Adaptation to changing environments across real geographies
Peter Ralph
ASN // Asilomar // January 13, 2016
Adaptation to climate change
Rapid climate change:
- occurring over tens of generations
- different environment \(\Rightarrow\) strong selective pressure
This talk: population genetics considerations.
What I'm not talking about:
- local adaptation
- plasticity
- genetic architecture
- population size dynamics
- interspecific interactions
What I am talking about:
- most organisms don't live on billiard tables
Questions
How does geography affect how adaptive variants
arise and
spread,
and how much variation is left afterwards?
Can adaptations spread?
- with moving environmental gradients
- or from locations of existing variants
Also relevant for:
- Do adaptive variants spread along wildlife corridors?
- What is the spatial resolution of adaptation?
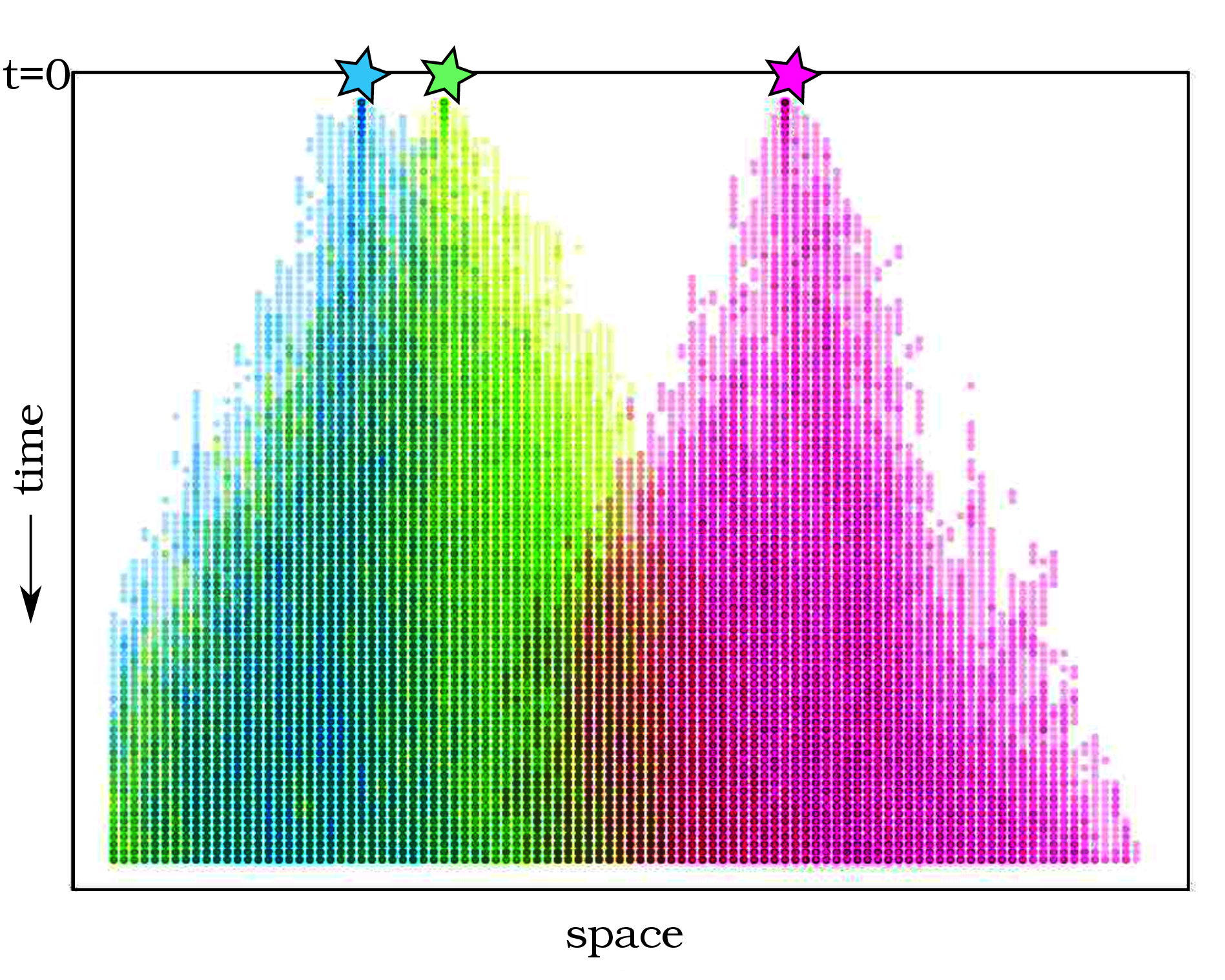
Population genetics wants to know:
population size
- availability of standing deleterious variation
- influx of new mutations
strength of selection
- probability of establishment of rare variants
- rate of spread of adaptive variants
rate of genetic drift
- rate of local loss of variation
- probability of establishment of rare variants
these are affected by
geography \({}+{}\) dispersal \({}+{}\) temporal dynamics

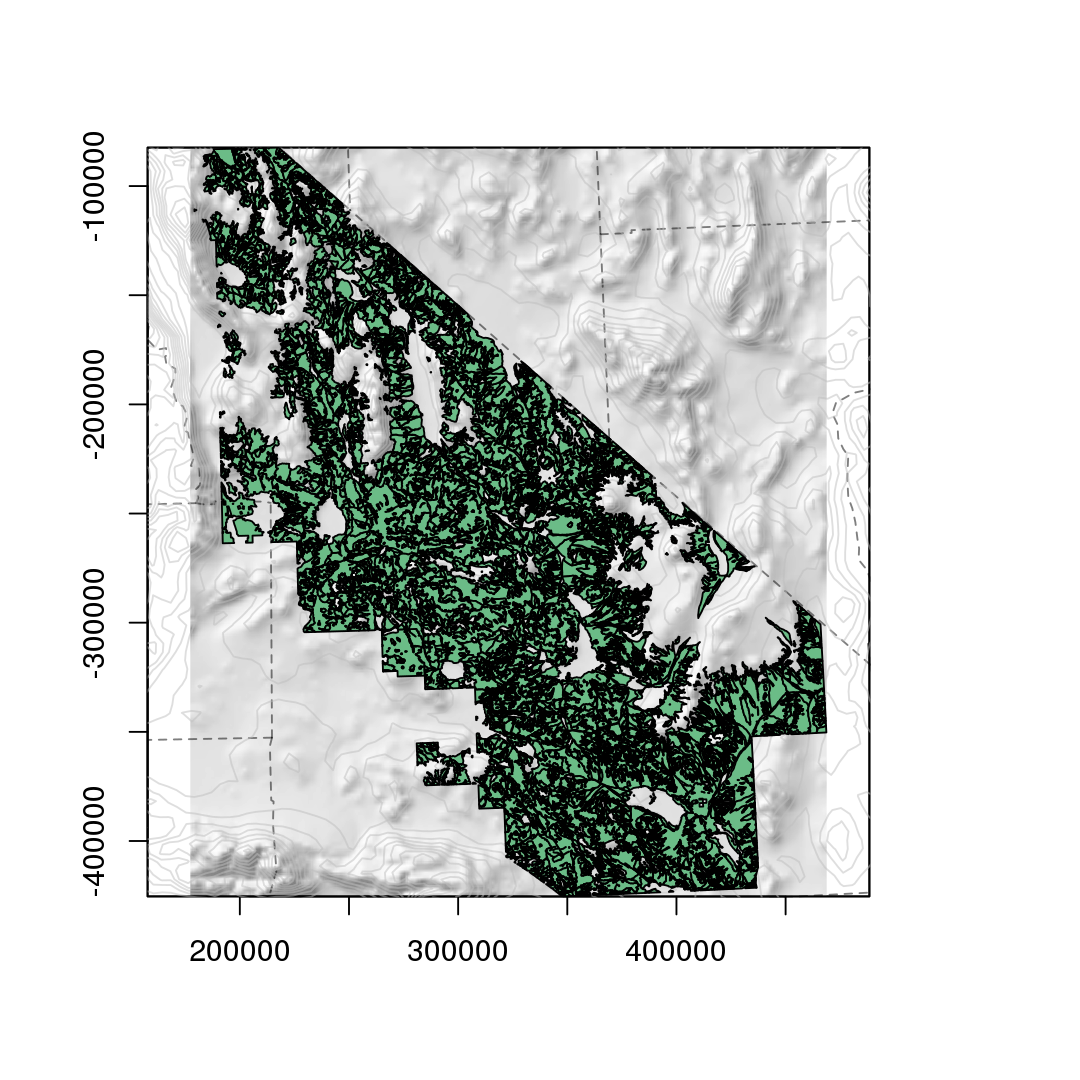
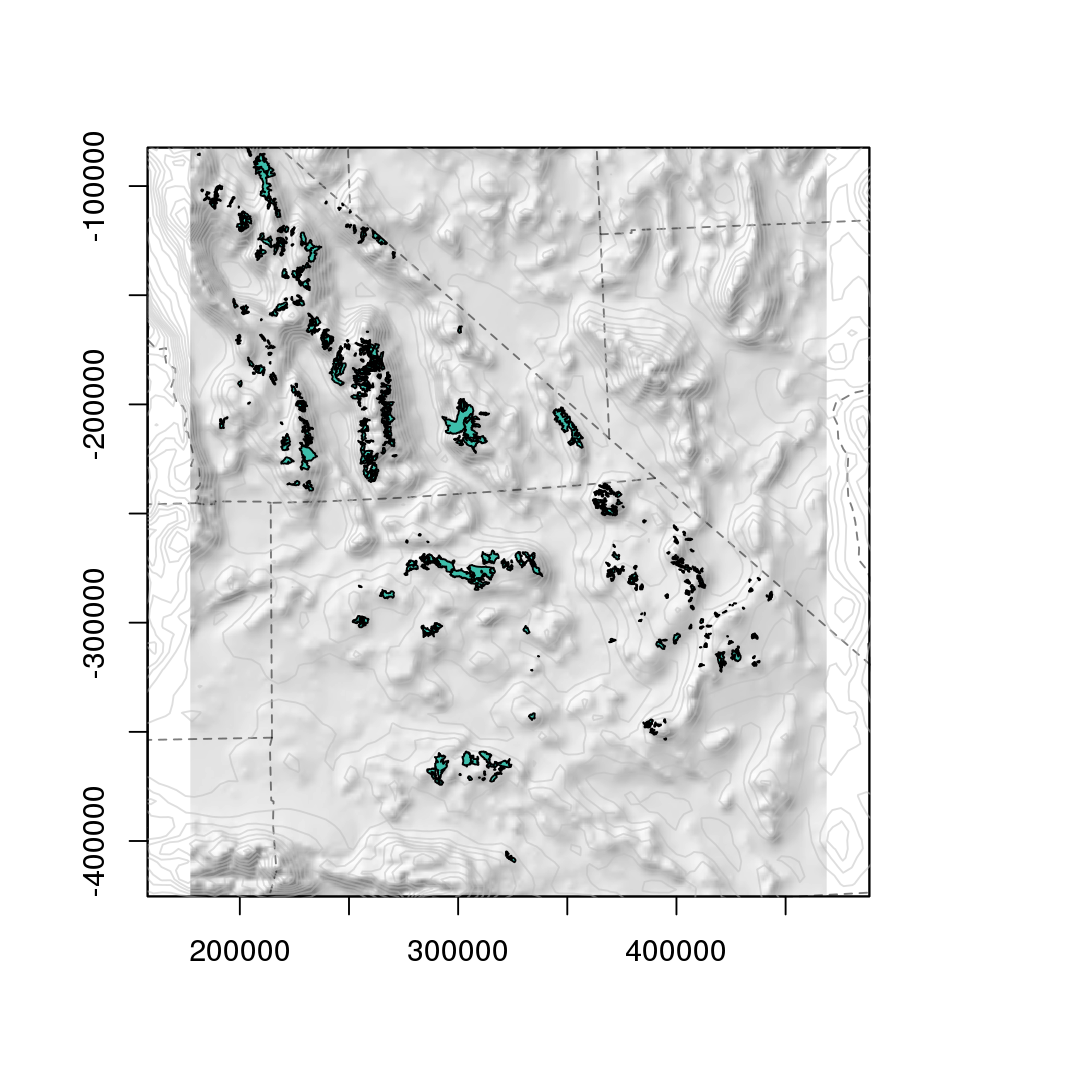
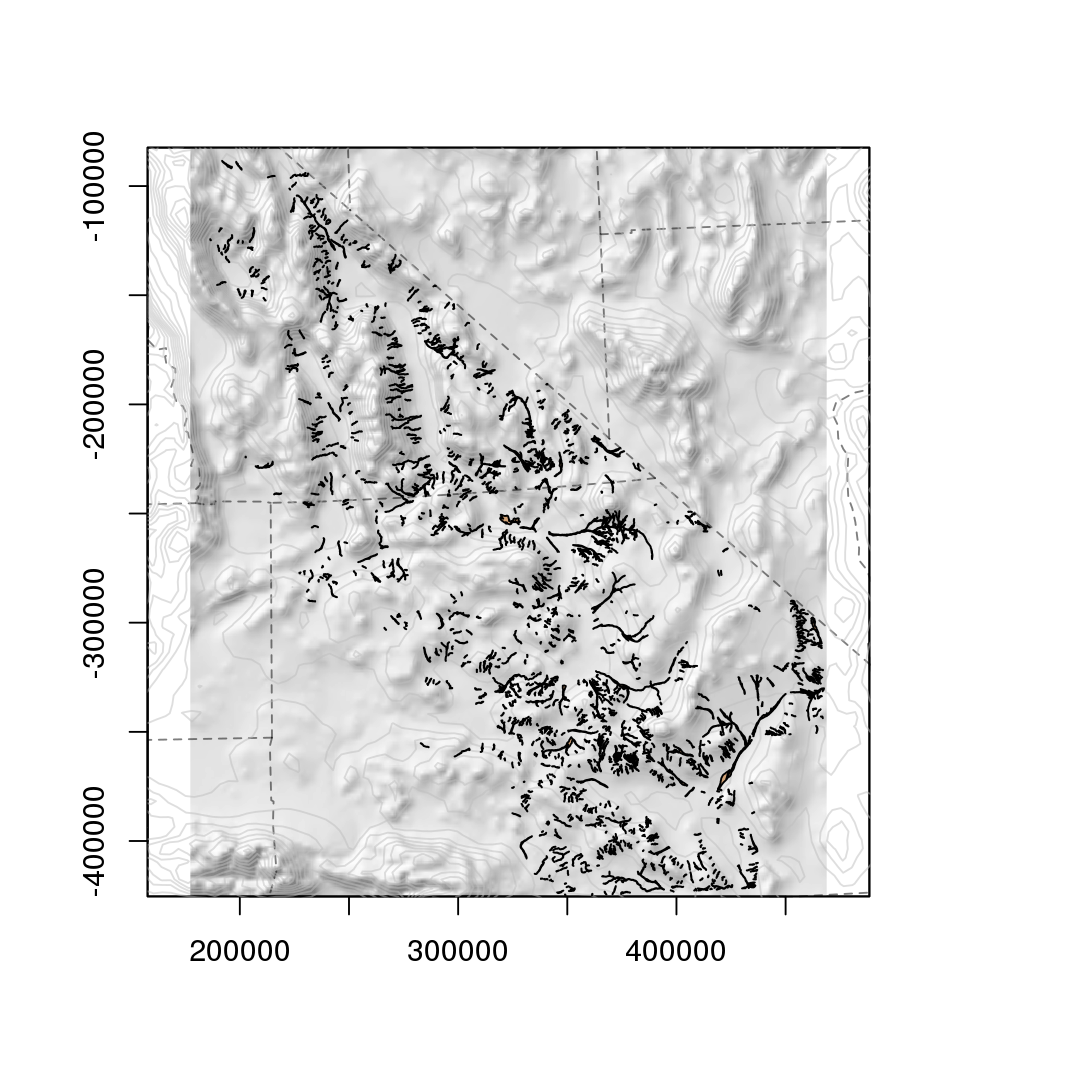
Mojave Desert habitats
Cal DFG; Todd Keeler-Wolf, CNPS (http://vegetation.cnps.org/)[http://vegetation.cnps.org/]
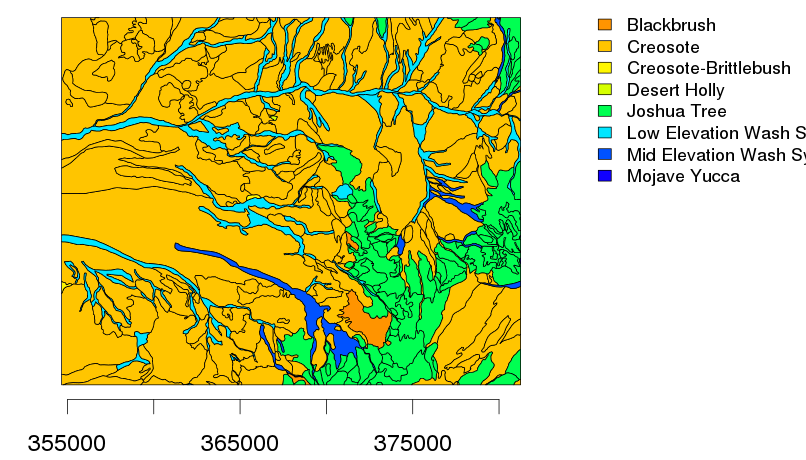
Zoomed-in (NVCS macrogroup):
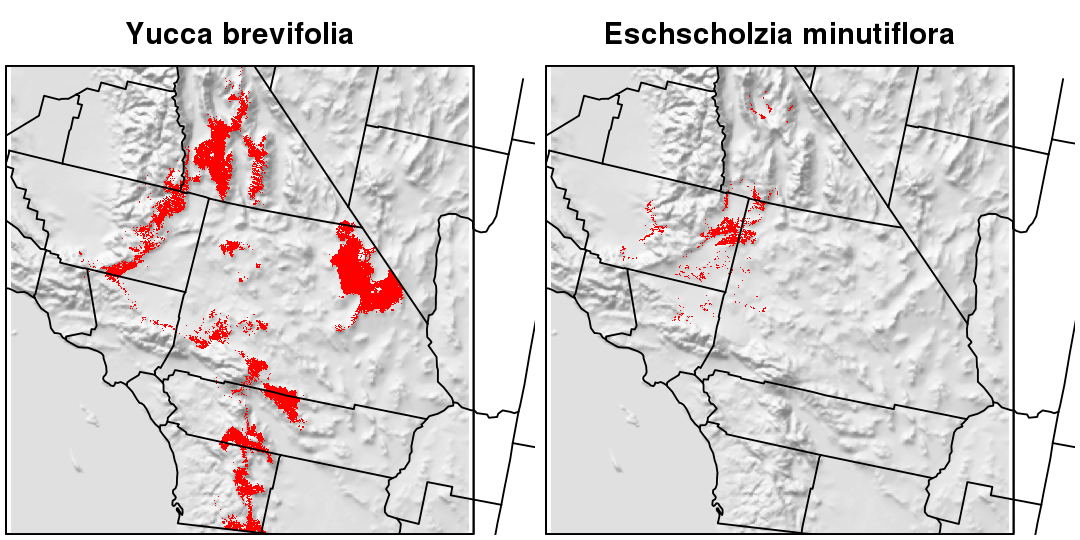
Environmental niche models: (Biogeography Lab, UCSB)
Demographic model
- 200m grid
- equilibrium density: 0.4 (low) or 16 (high) / ha
- R package: github.com/petrelharp/landsim
demography(
prob.seed = 0.2, fecundity = 100,
pollen.migration = migration(
kern = function (x) { exp(-sqrt(x)) },
sigma = 300, radius = 1200, normalize = NULL ),
seed.migration = migration(
kern = "gaussian", sigma = 100,
radius = 1200, normalize = 1 ),
prob.germination = vital(
function (N, ...) {
out <- r0 / ( 1 + rowSums(N)/carrying.capacity )
return( cbind( aa=out, aA=(1+s)*out, AA=(1+s)^2*out ) )
},
r0 = 0.01, s = 0.05 ),
prob.survival = 0.9,
genotypes = c("aa","aA","AA")
)Rate of genetic drift
Wright's neighborhood size:
\[ N_\text{loc} \propto \#\{ \text{ individuals within 1$\sigma$ } \}, \]
where
- \(\sigma\) is the dispersal distance
- individuals are haploid.
Local heterozygosity is \[ H_0 \propto \frac{N_\text{loc}}{C + N_\text{loc}}, \] where \(C\) depends on mutation rate and geometry.
(Barton, Depaulis, & Etheridge)
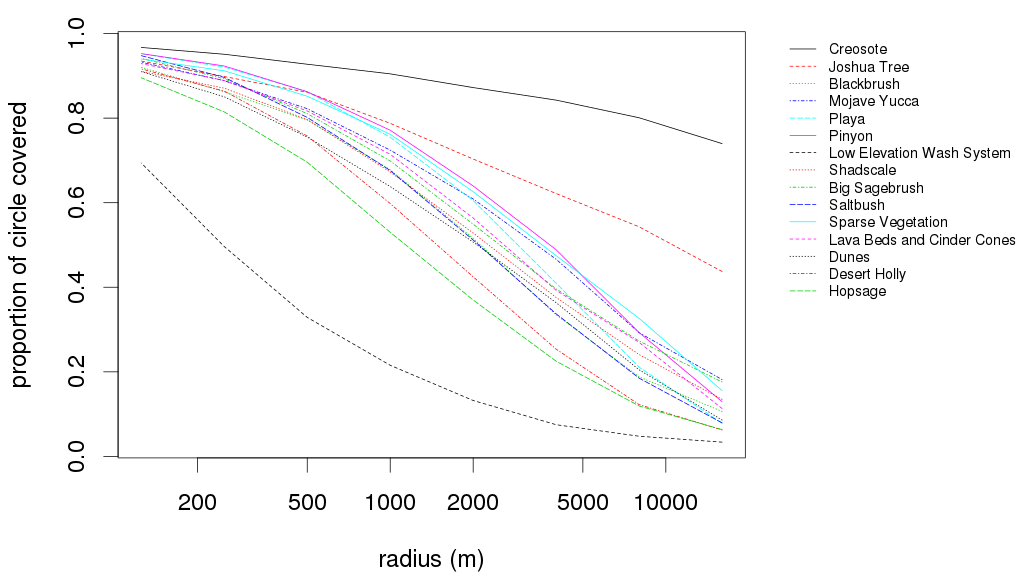
\(N_\text{loc}\) at different scales depends on population density and amount of nearby habitat:
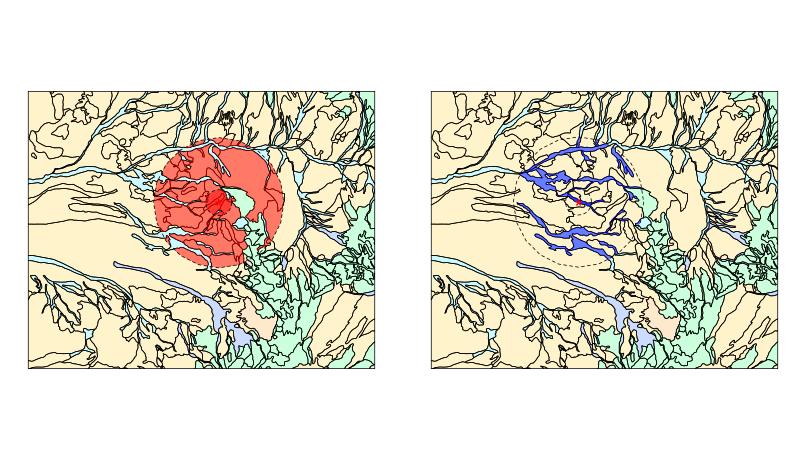
NVCS Macrogroup, central Mojave:
Creosote:
Blackbrush:
Wash:
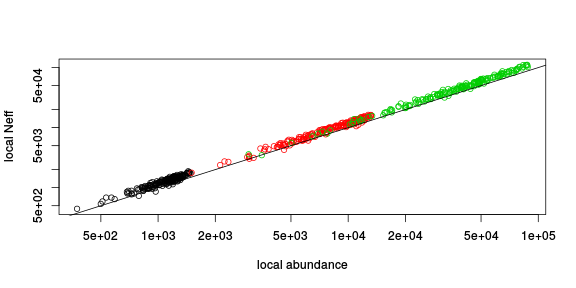
Genetic drift:
\[\var[p_{t+1}|p_t]/p_t(1-p_t) \text{ against } N_\text{loc}\]
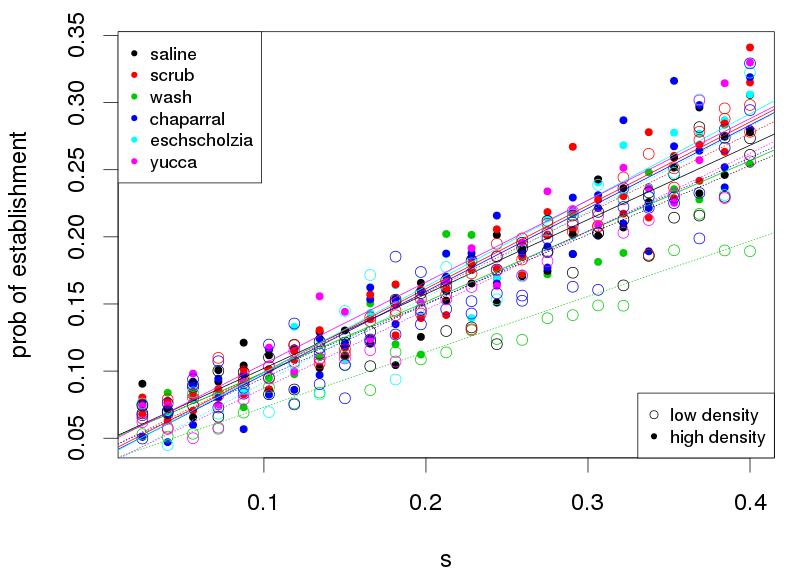
Probability of establishment
The probability of establishment of a single allele in a large population is \[ p_\text{estab} \approx 2 s / \nu , \]
- where \(\nu\) is the strength of drift
- \(s\) is growth rate when rare.
If \(s < 1/N_\text{loc}\), local inbreeding may reduce \(p_\text{estab}\).
Speed of spread
Alleles that are advantageous when rare spread, like wildfire. (a "pulled" wave)
Continuous habitats
- speed: \(\sigma \sqrt{2s}\) (Fisher/KPP)
- \(s\) is growth rate when rare
- takes 1-10 generations to move a dispersal distance
leptokurtic dispersal: patchy, accelerating (Mollison 1972)
slowed by drift
Huygens principle: the wave has to go around barriers (Möbius, Murray, & Nelson 2015)
- tortuosity: ratio of length of curve to distance between its ends
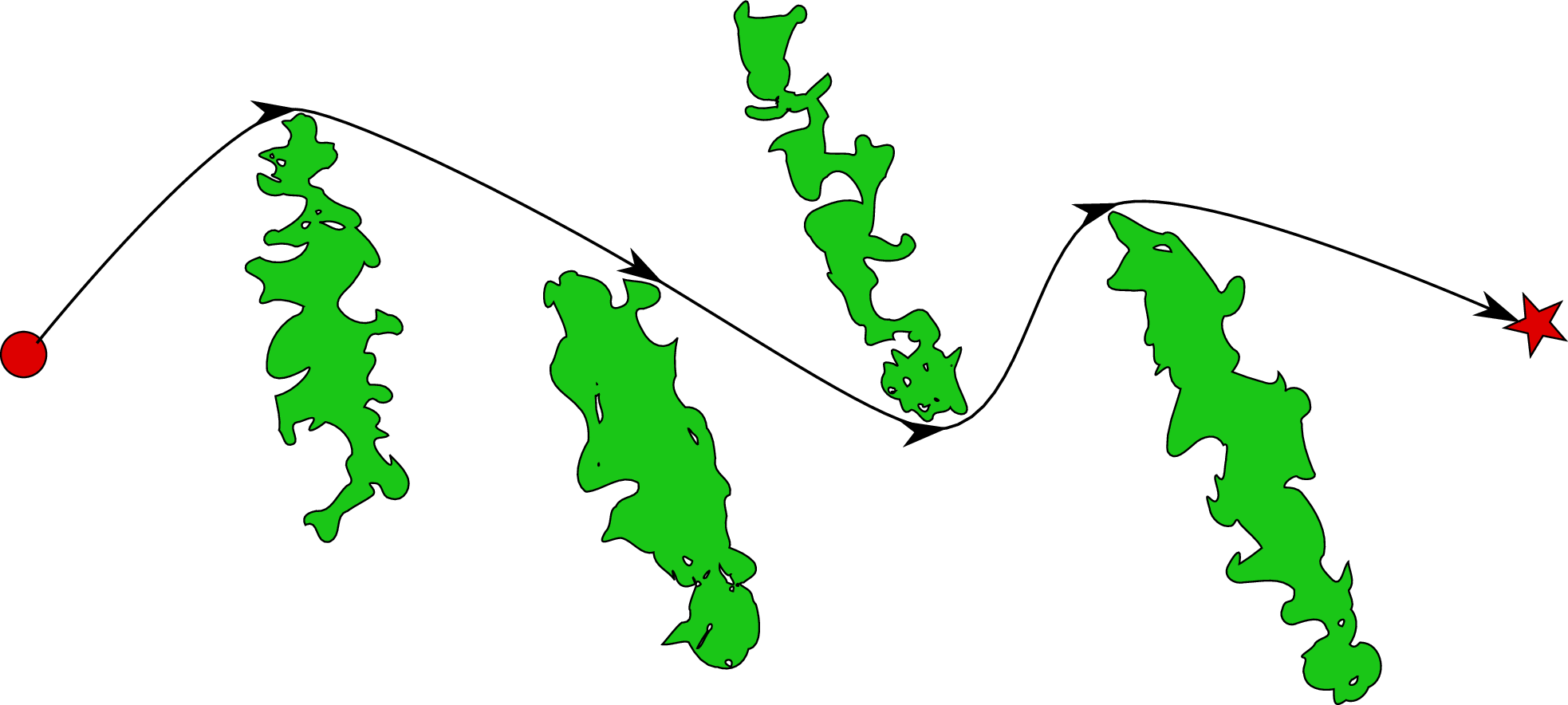
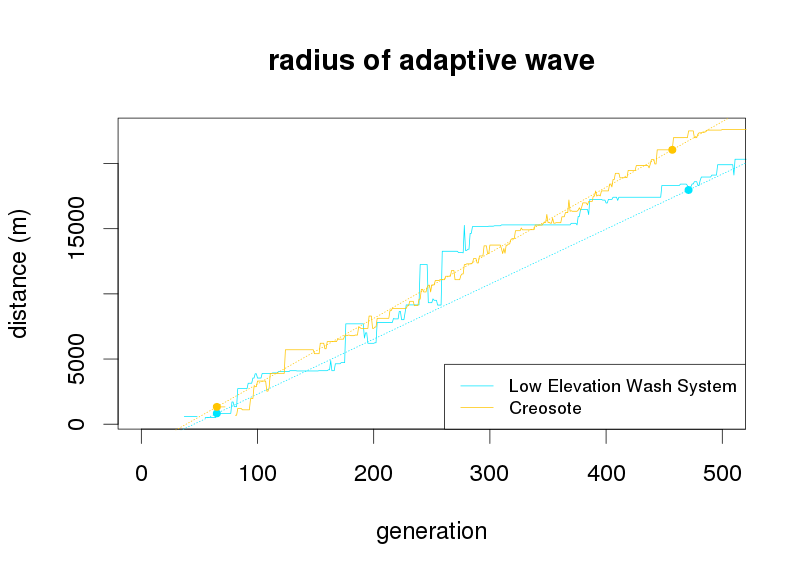
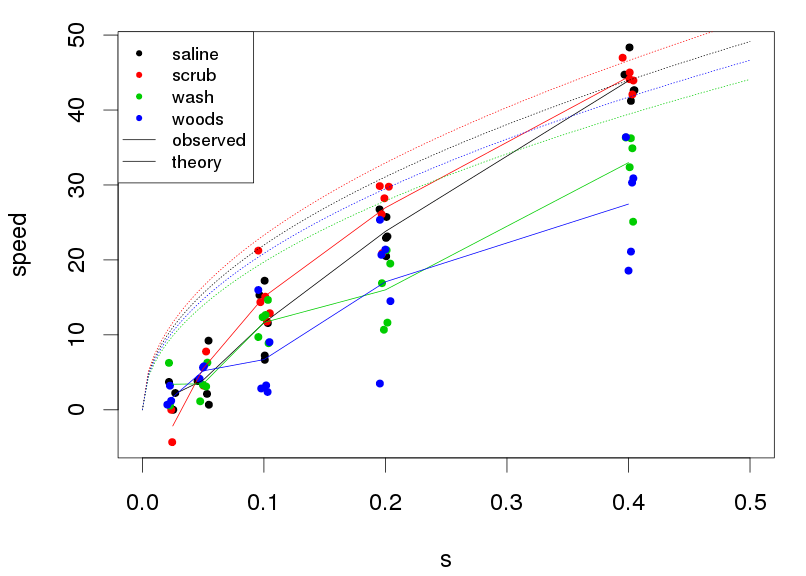
Speeds in different habitats:
Spread in patchy habitats
spread governed by arrival of migrants \({} \times p_\text{estab}\)
if gaps are totally uninhabitable (sparks carried by wind), depends on long distance dispersal
if growth rate in gaps is \(1-m\) (flammable but fire dies out) rate of migrant families is
\[\propto e^{-x \sqrt{2m}/\sigma}\]
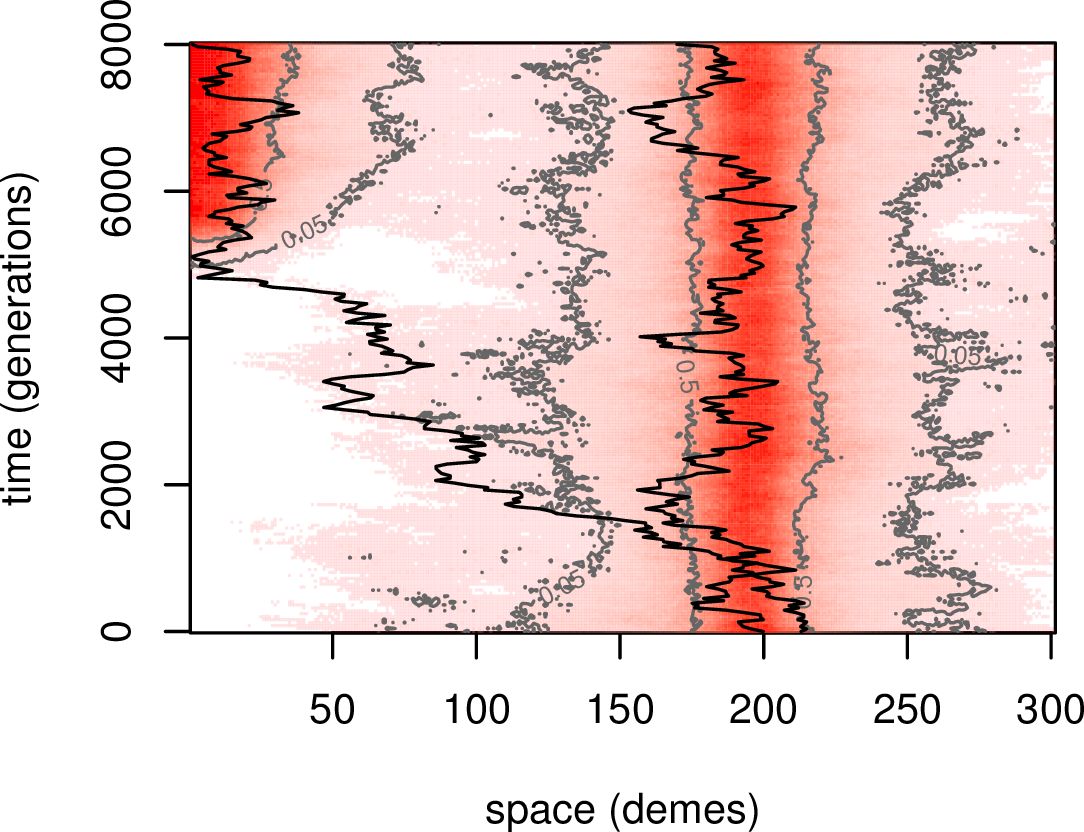
Both depend critically on dispersal mechanism.
Conclusions
Adaptation in connected habitats depends on habitat shape, but only weakly.
Adaptation is strongly affected by
- connectivity
- long-distance dispersal
- population size
- ecological interactions
Notes:
- Allee affects?
- Ubiquitous, polygenic variation?
- Many habitats are patchy: are they still connected?
- Shape of isolation by distance?
Thanks!
- Erik Lundgren (USC)
- Julie Evens (CNPS)
- Greg Suba (CNPS)
R's GIS tools:
sp,raster,rgeos, ...- NSF: ABI
Sloan Foundation
The R package: github.com/petrelharp/landsim