What’s the effect of dispersal?
How gene flow depends on ecology.
Peter Ralph
University of Oregon
Institute of Ecology and Evolution
5th Workshop Probability and Evolution
slides: github:petrelharp/cirm_2021_talk
Joint work with:
Alison Etheridge
Tom Kurtz
Ian Letter
Terence Tsui


title text: “On one hand, every single one of my ancestors going back billions of years has managed to figure it out. On the other hand, that’s the mother of all sampling biases.”
The “problem” of geography
Some PopGen in Space

image by Graham Coop
“Isolation by distance”
… describes the relationship of genetic distance and geographic distance, where \[\begin{aligned} d(i,j) &= \text{(genetic distance between individuals $i$ and $j$)} \\ &= \frac{\text{number of nucleotide differences}}{\text{length of the genome}} . \end{aligned}\]
The Wright-Malecót formula says that in 2D: \[\begin{aligned} \mathbb{E}[1 - d(i, j)] &\approx \frac{1}{\mathcal{N} + \log(\sigma_e / (\kappa \sqrt{2\mu}))} K_0\left( \frac{\sqrt{2\mu}|x_i-x_j|}{\sigma_e} \right) . \end{aligned}\] (see e.g., Barton, Depaulis & Etheridge (2002); Smith & Weissman 2020)
 But: what’s \(\sigma_e\)?
But: what’s \(\sigma_e\)?
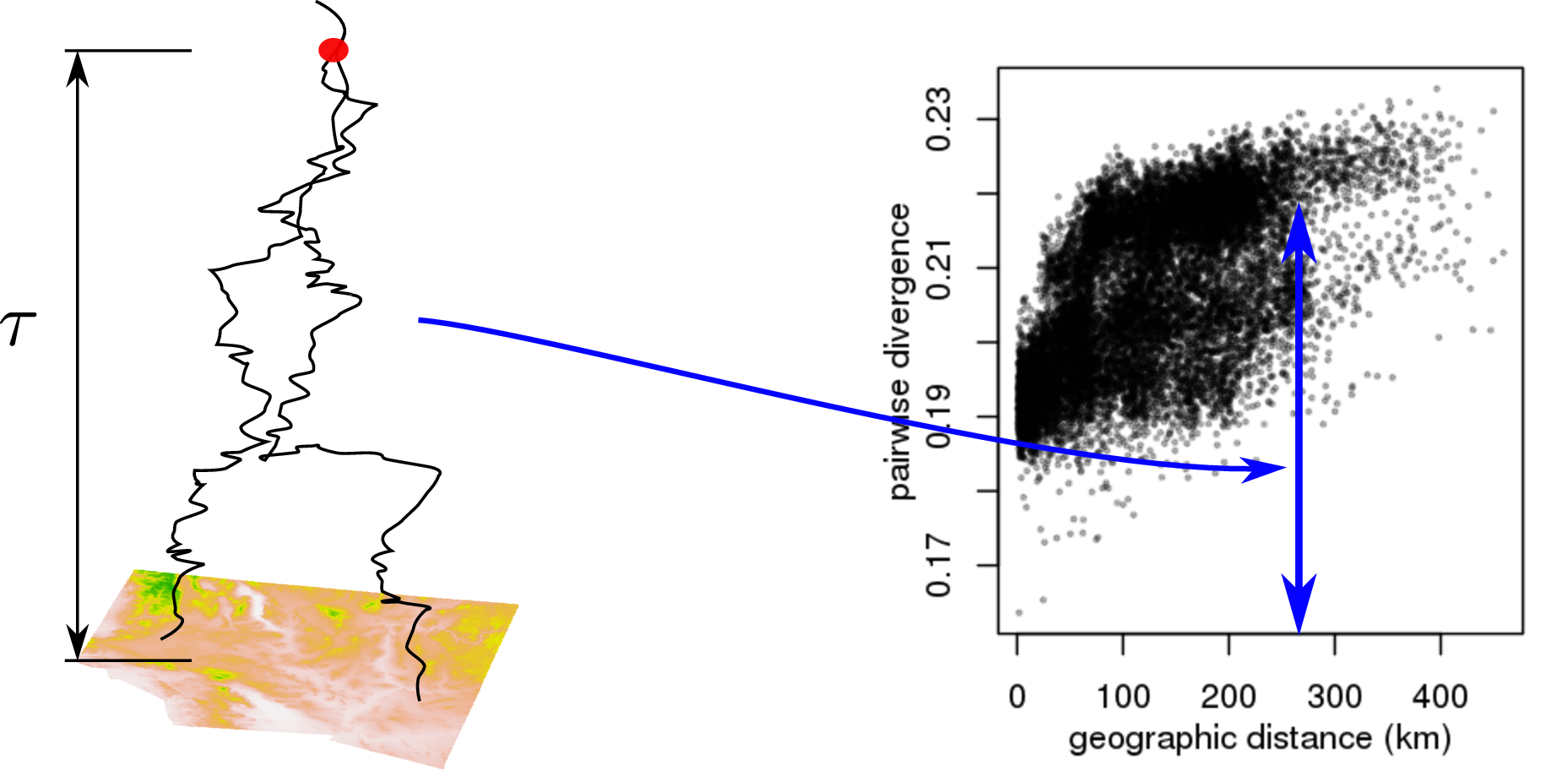
Tracing back lineages
The lineage of a bit of modern genome is \[\begin{aligned} L_t = \text{(location of the genetic ancestor at time $t$ ago)} . \end{aligned}\]
Statistical properties of \(L\) tell us about:
gene flow
long-term fitness
\(\sigma_e\)
Questions:
The dispersal distance is \[\begin{aligned} \sigma^2 &= \text{(mean squared displacement} \\ &\qquad \text{between parent and offspring)} \end{aligned}\] and the effective dispersal distance is \[\sigma^2_e = \lim_{t \to \infty} \frac{1}{t} \mathbb{E}[L_t^2] .\]
- What determines the sign of \[\sigma_e^2 - \sigma^2 ? \]
- How does \(L_t\) move, anyhow?
A discrete model
discrete space and time,
varying population sizes,
nonoverlapping generations, with movement only at reproduction.

Suppose: \[\begin{aligned} N(x,t) &= \text{(number of individuals $t$ generations ago at $x$)} \\ m(x, y) &= \text{(proportion of seeds from $x$ that go to $y$)} \end{aligned}\]
… and surviving individuals are uniform choices out of available seeds.
and so \[\begin{aligned} \mathbb{P}\{ L_t = y \;|\; L_{t-1} = x \} &= \frac{ N(y,t) m(y, x) } { \sum_z N(z,t) m(z, x) } . \end{aligned}\]
Assume \(L_t\) is Markov given \(N\) (generally requires \(N\) to be large).
Patchy habiat: consider a weed
Assume a 1D grid of populations, and
- two habitat types: \(N(x,t) \in \{G, B\}\), with \(G \gg B\),
- For each \(t\), the environment \((\ldots, N(x-1, t), N(x, t), N(x+1, t), \ldots)\) is a stationary Markov chain with transition matrix
\[\begin{aligned} P = \begin{bmatrix} 1-p & p \\ q & 1-q \\ \end{bmatrix} . \end{aligned}\]
- The environment at each time \(t\) is independent of everything else.
And,
- \(m(x,y) = 1/3\) if \(|x-y| \le 1\).
\[\begin{aligned} \text{Note: forwards dispersal has } \sigma^2 = \frac{2}{3} . \end{aligned}\]
Then \(L_{t+1} \; | L_t = x\):
- chooses a “good” patch uniformly from \(\{x-1, x, x+1\}\), if any;
- if not, chooses a neighboring patch uniformly.
What is \(\sigma^2_e\)?
| habitat | probability | \(\mathbb{E}[(L_1 - L_0)^2]\) |
|---|---|---|
| GGG | \(\frac{p}{p+q} (1-q)^2\) | 2/3 |
| GGB/BGG | \(\frac{p}{p+q} (1-q)q\) | 1/2 |
| GBB/BBG | \(\frac{p}{p+q} q(1-p)\) | 1 |
| GBG | \(\frac{p}{p+q} qp\) | 1 |
| BGB | \(\frac{q}{p+q} pq\) | 0 |
| BBB | \(\frac{q}{p+q} (1-p)^2\) | 2/3 |
\[\begin{aligned} \mathbb{E}[(L_1 - L_0)^2] = \frac{2}{3} + \frac{ pq } {3 (p + q) } \left(1 - (p + q)\right) . \end{aligned}\]
\[\begin{aligned} &\sigma^2_e - \sigma^2 \\ &\qquad {} = \frac{ pq } {3 (p + q) } \left(1 - (p + q)\right) . \end{aligned}\] and so \[\begin{aligned} \sigma_e > \sigma \qquad \text{iff} \quad p + q < 1, \end{aligned}\]
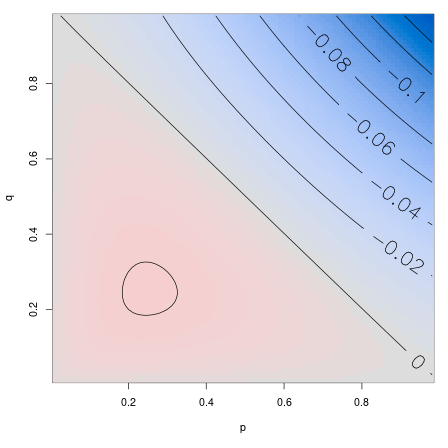
\[\begin{aligned} &\sigma^2_e - \sigma^2 \\ &\qquad {} = \frac{ pq } {3 (p + q) } \left(1 - (p + q)\right) . \end{aligned}\] and so \[\begin{aligned} \sigma_e > \sigma \qquad \text{iff} \quad p + q < 1, \end{aligned}\]
So: the random environment can either slow down or speed up a lineage
… even with no temporal correlations!

What about temporal correlations?
Now suppose
The environment is a stationary, reversible Markov process on \(\{G, B\}^\mathbb{Z}\).
For each \(t\), the environment \(N(t, \cdot)\) is a stationary Markov chain with transition matrix as before.
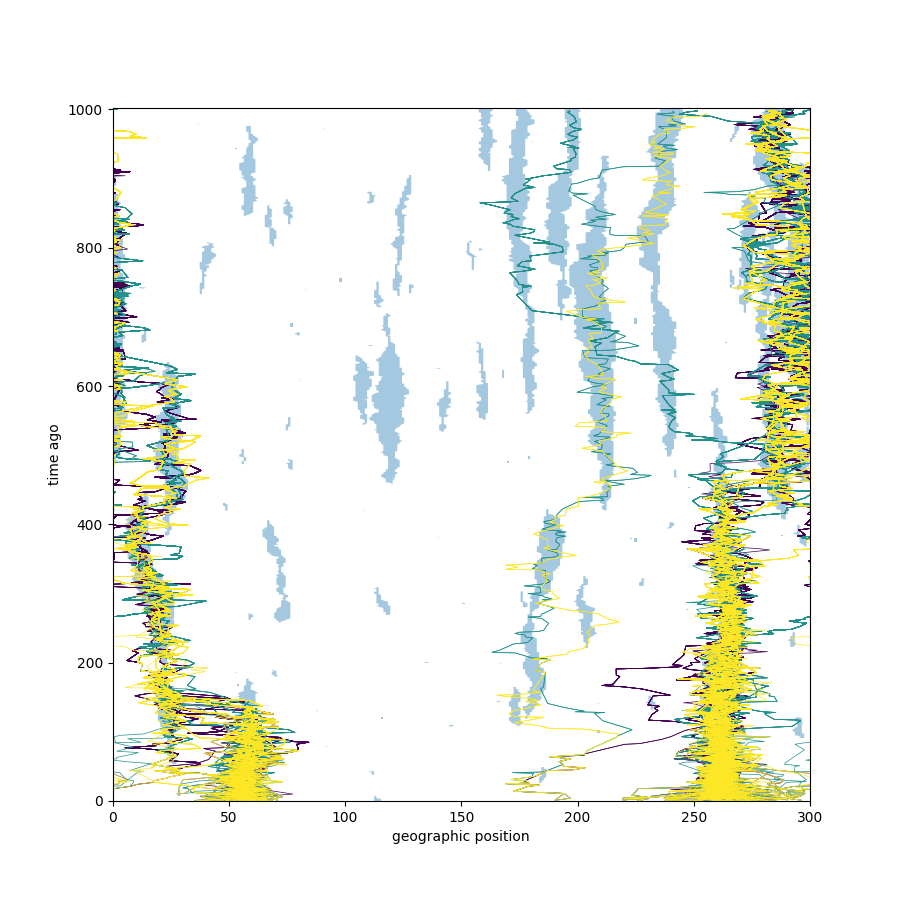
What about temporal correlations?
Now suppose
The environment is a stationary, reversible Markov process on \(\{G, B\}^\mathbb{Z}\).
For each \(t\), the environment \(N(t, \cdot)\) is a stationary Markov chain with transition matrix as before.
Numerically: changing temporal correlations can also increase or decrease speed.
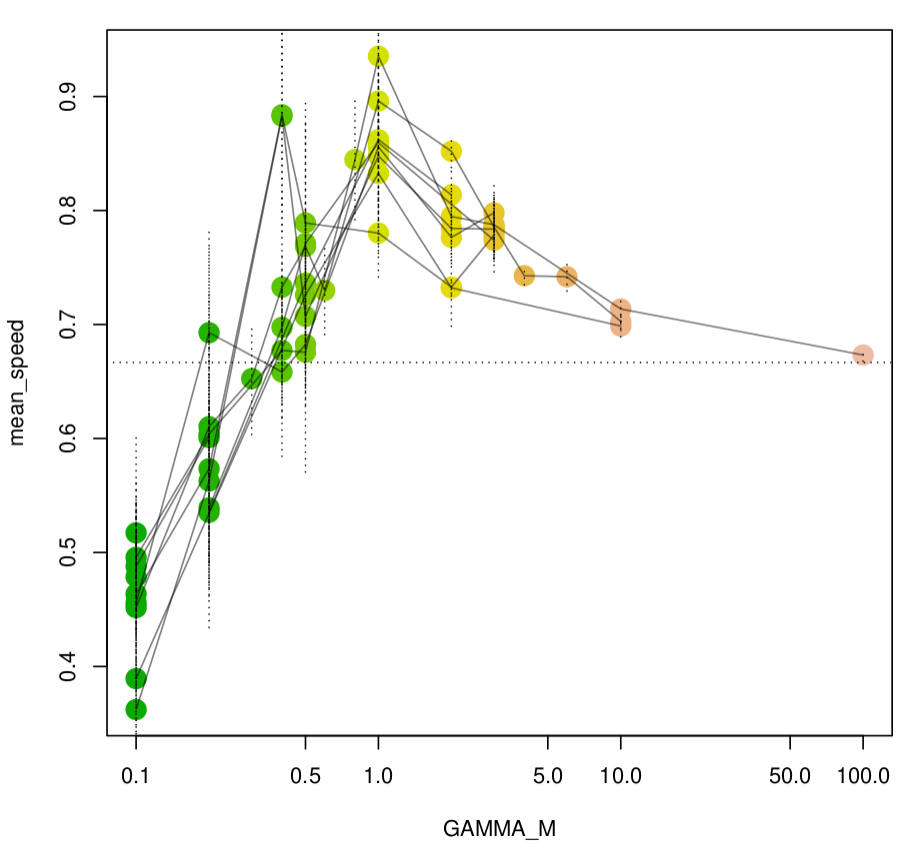
How do lineages move, anyways?
Next: continuous space (and, time).
The model:
- \(N\): scaling factor for density
- \(\eta_t\): point measure with mass \(1/N\) for each individual on \(\mathbb{R}^d\)
- \(\gamma(x, \eta_t)\): per capita birth rate at \(x\)
- \(q(x, dy)\): probability a juvenile disperses to \(y\)
- \(r(y, \eta_t)\): juvenile establishment probability at \(y\)
- \(\mu(x, \eta_t)\): death rate at \(x\)
The (forwards) dispersal distance is: \[ \sigma^2 = \int |y-x|^2 q(x, dy) .\]
Birth, establishment, and establishment rates depend on local population densities (like Bolker-Pacala):
- \(p_\epsilon\): the heat kernel at time \(\epsilon\)
- \(p_\epsilon * \eta_t(x)\): “local” population density at \(x\)
- \(\sqrt{\epsilon}\): interaction distance
Vital rates at \(x\) will depend on \(\eta\) through \(p_\epsilon * \eta(x)\).
For instance
Mortality increases with crowding: \(\gamma\) and \(r\) are constant, while \[\begin{aligned} \mu(x, \eta) &= \mu(x) \left( 1 - \frac{1}{1 + \exp(p_\epsilon * \eta(x))} \right) . \end{aligned}\]
Or, for instance
Fecundity decreasing with crowding: \(\mu\) and \(r\) are constant, while \[\begin{aligned} \gamma(x, \eta) &= \gamma(x) \left( \frac{1}{1 + \exp(p_\epsilon * \eta(x))} \right) . \end{aligned}\]
Mean change in \(\eta\):
\[\begin{aligned} & \frac{1}{N} \times N \eta(y) \gamma(y, \eta) \; \hphantom{q(y, dx)} &\qquad &\text{(birth at $y$)} \\ & \hphantom{\frac{1}{N}} \int \; \hphantom{N \eta(y) \gamma(y, \eta)} \; q(y, dx) r(x, \eta) &\qquad &\text{(dispersal to $x$)} \end{aligned}\]
and
\[\begin{aligned} & {} - \frac{1}{N} \times N \eta (x) \mu(x, \eta) & \qquad &\text{(death)} \end{aligned}\]
The mean measure
So: for a test function \(f\), \[\begin{aligned} & \lim_{t \searrow 0} \frac{1}{t} \left. \mathbb{E} \left[ \int f(x) \eta_{t}(dx) - \int f(x) \eta_0(dx) \;|\; \eta_0 = \eta \right] \right\vert_{t=0} \\ &\qquad = \int \int f(x) r(x, \eta) q(y, dx) \gamma(y, \eta) \eta(dy) \\ &\qquad \qquad {} - \int f(x) \mu(x, \eta) \eta(dx) . \end{aligned}\]
\[\begin{aligned} &{} = \int \left\{ \int \left( f(x) r(x, \eta) - f(y) r(y, \eta) \right) q(y, dx) \right\} \gamma(y, \eta) \eta(dy) \\ &\qquad \qquad {} + \int f(x) \left\{ r(x, \eta) \gamma(x, \eta) - \mu(x, \eta) \right\} \eta(dx) . \end{aligned}\]
What about noise?
Since reproduction produces single offspring,
\[\begin{aligned} & \lim_{t \searrow 0} \frac{1}{t} \left. \mathbb{E} \left[ \left( \int f(x) \eta_{t}(dx) - \int f(x) \eta_0(dx) \right)^2 \;|\; \eta_0 = \eta \right] \right\vert_{t=0} \\ &\quad {} = \frac{1}{N} \left\{ \int \int f^2(x) r(x, \eta) q(y, dx) \gamma(y, \eta) \eta(dy) \right. \\ &\qquad \qquad \left. {} + \int f^2(x) \mu(x, \eta) \eta(dx) \right\} \end{aligned}\]
\[\begin{aligned} {} \propto \frac{1}{N} . \hphantom{ \left\{ \int \int f^2(x) r(x, \eta) q(y, dx) \gamma(y, \eta) \eta(dy) \right\} } \end{aligned}\]
Diffusion limits
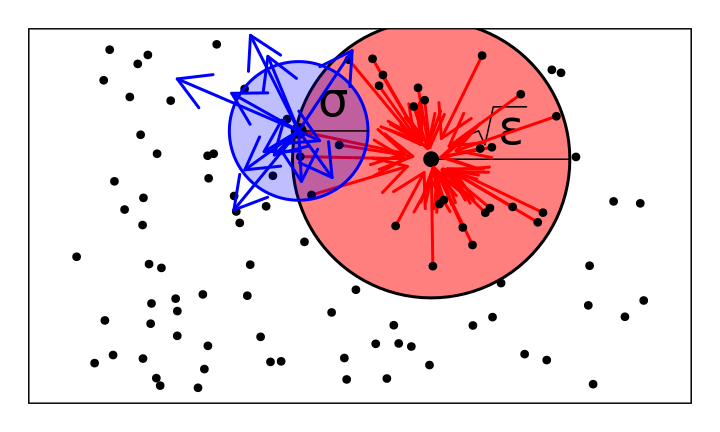
As \(N \to \infty\), also rescale time by \(\theta\), and let e.g., \[ r_\theta(x, \eta) \to r(x, \eta) \qquad \text{as } \theta \to \infty . \]
As \(\theta \to \infty\), to see lineages moving, we take \(\sigma = 1/\sqrt{\theta}\), so that \[ \theta \int (g(y) - g(x)) q_\theta(x, dy) \to \frac{1}{2} \Delta g(x) , \]
and population density changes on a time scale of \(\theta\) generations: \[ \theta\left( r_\theta(x, \eta) \gamma_\theta(x, \eta) - \mu_\theta(x, \eta) \right) \to F(x, \eta) . \]
Suppose also the population measure converges:
\[ \eta \to \Xi \qquad \text{as} \qquad \theta, N \to \infty \]
and so \[\begin{aligned} & \lim_{t \searrow 0} \frac{1}{t} \left. \mathbb{E} \left[ \int f(x) \eta_{t}(dx) - \int f(x) \eta_0(dx) \;|\; \eta_0 = \eta \right] \right\vert_{t=0} \\ &\qquad \to \int \left\{\vphantom{\int} \gamma(x, \Xi) \Delta\left( f(\cdot) r(\cdot, \Xi) \right)\!(x) \right. \\ &\qquad \qquad \qquad \left. \vphantom{\int} + f(x) F(x, \Xi) \right\} \Xi(dx) . \end{aligned}\]
Three types of limits
The limit acts like \[
``\; \dot \Xi = r \Delta(\gamma \Xi) + F \Xi . \text{''}
\] … but recall that the coefficients are “nonlocal”:
\(r\) may be a function of \(p_\epsilon * \Xi\).
Some options for \(\Xi\):
Stochastic, nonlocal coefficients. (superprocess limit)
Deterministic, nonlocal coefficients.
Deterministic, local coefficients. (PDE limit)
Superprocess limit:
Quadratic variation of the limit is nonzero if \[ \frac{N}{\theta} \to \rho, \] for some \(\rho > 0\).
In other words, since \(\sigma = 1/\sqrt{\theta}\), Wright’s neighborhood size is: \[\begin{aligned} \mathcal{N} &:= \text{(mean number of individuals within distance $\sigma$)} \\ &\propto N \sigma^d \end{aligned}\] … which is equal to \(\rho\) in \(d=2\).
Deterministic limit: \(\theta/N \to 0\)
If the limiting measure has density \(\Xi_t(x) dx\), then it’s a weak solution to \[\begin{aligned} \frac{d}{dt} \Xi_t(x) &= r(x, \Xi) \Delta\left( \gamma(\cdot, \Xi_t) \Xi_t(\cdot) \right)(x) + F(x, \Xi_t) \Xi_t(x) . \end{aligned}\]
i.e., \[\begin{aligned} \dot \Xi = r \Delta\left( \gamma \Xi \right) + F \Xi . \end{aligned}\]
PDE limit?
Recall that e.g., \[\begin{aligned} r(x, \eta) = r(p_\epsilon * \eta(x)) . \end{aligned}\]
… can we also take \(\epsilon \to 0\), getting \[\begin{aligned} \frac{d}{dt} \Xi_t(x) &= r(\Xi_t(x)) \Delta\left( \gamma(\Xi_t(\cdot)) \Xi_t(\cdot) \right)\!(x) \\ &\qquad {} + F(\Xi_t(x)) \Xi_t(x) ? \end{aligned}\]
For fixed \(\epsilon\), we have that \[ \eta_\epsilon \to \Xi_\epsilon \qquad \text{as } N, \theta \to \infty. \]
We need \(p_\epsilon * \eta_\epsilon(x) \to \Xi(x)\), e.g., \[\begin{aligned} & (p_\epsilon * \eta_\epsilon - p_\epsilon * \Xi_\epsilon) \hphantom{+ (p_\epsilon * \Xi_\epsilon - p_\epsilon * \Xi) + (p_\epsilon * \Xi - \Xi)} \\ &\hphantom{(p_\epsilon * \eta_\epsilon - p_\epsilon * \Xi_\epsilon)} + (p_\epsilon * \Xi_\epsilon - p_\epsilon * \Xi) \hphantom{+ (p_\epsilon * \Xi - \Xi) } \\ &\hphantom{(p_\epsilon * \eta_\epsilon - p_\epsilon * \Xi_\epsilon) + (p_\epsilon * \Xi_\epsilon - p_\epsilon * \Xi)} + (p_\epsilon * \Xi - \Xi) \\ &\qquad \to 0 \qquad \text{as} \qquad N, \theta \to \infty, \qquad \epsilon \to 0 . \end{aligned}\]
What about the lineages?
Goal: rescale population densities while retaining the notion of lineages.
Method: a lookdown construction, following Kurtz & Rodrigues 2011 and Etheridge & Kurtz 2019.
… this also gives us tightness for the population processes themselves!
Deterministic, nonlocal limit:
Theorem: Suppose that for fixed \(\epsilon\), \[\begin{aligned} r(x, \eta) &= r(x), \\ \gamma_\theta(x, \eta) &= \gamma(p_\epsilon * \eta(x)) + \frac{G(p_\epsilon * \eta(x))}{\theta r(x)} \\ \mu_\theta(x, \eta) &= \gamma(p_\epsilon * \eta(x)) + \frac{H(p_\epsilon * \eta(x))}{\theta} \\ q_\theta(x, dy) &= p_{1/\theta}(x, dy) , \end{aligned}\] with \(\gamma\), \(G\), \(H\), and \(r\) uniformly bounded and Lipschitz continuous, and \(0 < r_0 < r(x) \le 1\) twice diff’able. Then a lookdown construction with maximum level \(N \to \infty\), with \(\theta \to \infty\) and \(\theta / N \to 0\), converges to a measure-valued process \((\eta_t^\infty)_{t \ge 0}\).
(theorem, continued)
The limit is a Cox measure with intensity a product of \(\Xi_t \times \Lambda\), and for every continuous, bounded \(f : \mathbb{R}^d \to \mathbb{R}_+\), \[\begin{aligned} & \int f(x) \Xi_t(dx) - \int f(x) \Xi_0(dx) \\ &= \int_0^t \int \gamma(p_\epsilon * \Xi_s(x)) \Delta \left( f(\cdot) r(\cdot) \right)(x) \\ {}&\qquad + f(x) \left\{ G(p_\epsilon * \Xi_s(x)) - H(p_\epsilon * \Xi_s(x)) \right\} \Xi_s(dx) ds . \end{aligned}\]
PDE limit
Theorem: Suppose that \(r(x) = 1\) and \[\begin{aligned} \gamma_\theta(x, \eta) &= 1 + \frac{G(p_\epsilon * \eta(x))}{\theta} \\ \mu_\theta(x, \eta) &= 1 + \frac{H(p_\epsilon * \eta(x))}{\theta} \\ q_\theta(x, dy) &= p_{1/\theta}(x, dy) , \end{aligned}\] with \(G\), \(H\) positive, Lipschitz continuous with \(G(1) = H(1)\) and such that \[ G(u), H(u) \le C \left( 1 + u^p \right) . \]
(theorem, continued)
Then a lookdown construction with maximum level \(N\), as \(N, \theta \to \infty\), if \(\theta/N \to 0\) and \[ \frac{\theta}{N \epsilon^{3dp/2}} + \frac{1}{\theta \epsilon^{dp/2}} \to 0 , \] converges to a measure-valued process \((\eta_t^\infty)_{t \ge 0}\).
The limit is a Cox measure with intensity a product of \(\Xi_t \times \Lambda\), where \(\Xi_t\) has a density that is a weak solution to \[\begin{aligned} \frac{d}{dt} \Xi &= \Delta \Xi + (G(\Xi) - H(\Xi)) \Xi, \end{aligned}\] for \(x \in \mathbb{R}^d\) and \(t > 0\) and appropriate initial conditions.
A note of caution

Gilia Patterson
death: \(\mu = 0.3\) per generation
establishment: \(r = 0.7\)
dispersal: Gaussian with SD \(\sigma\)
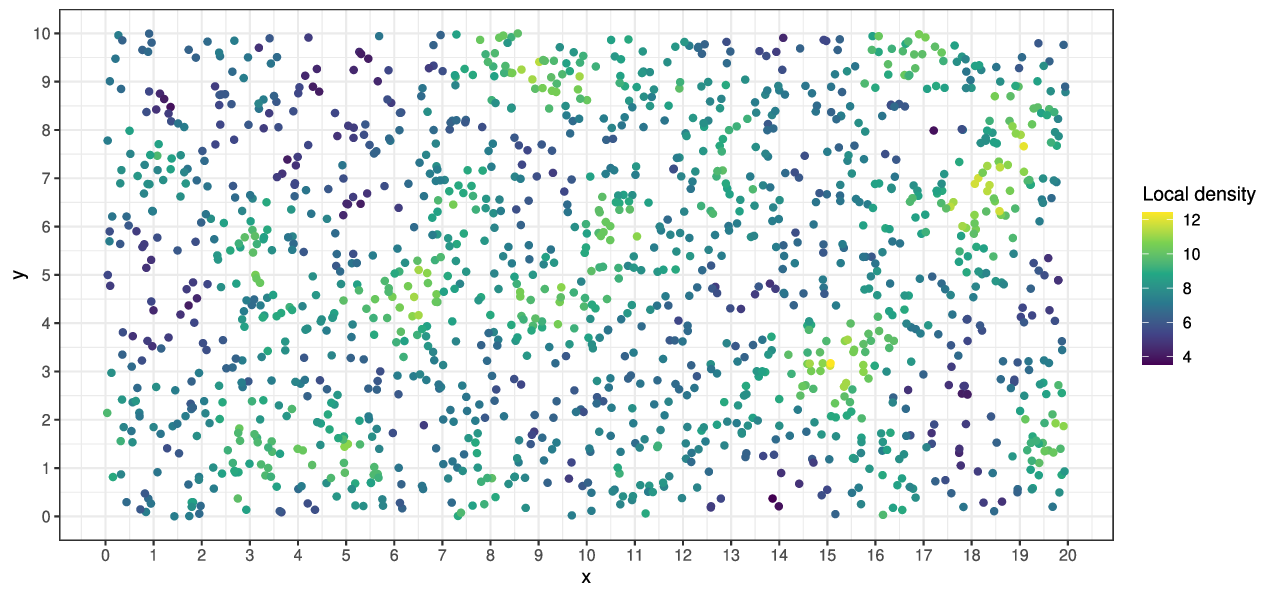
local density: in circle of radius \(\epsilon\)
reproduction: with \(K=2\), \(\lambda=3\), \[ \gamma = \frac{\lambda}{1 + \text{(local density)}/K} \]
non-spatial equilibrium density: \[ K \left( \frac{\lambda}{1 - r} - 1 \right) .\]
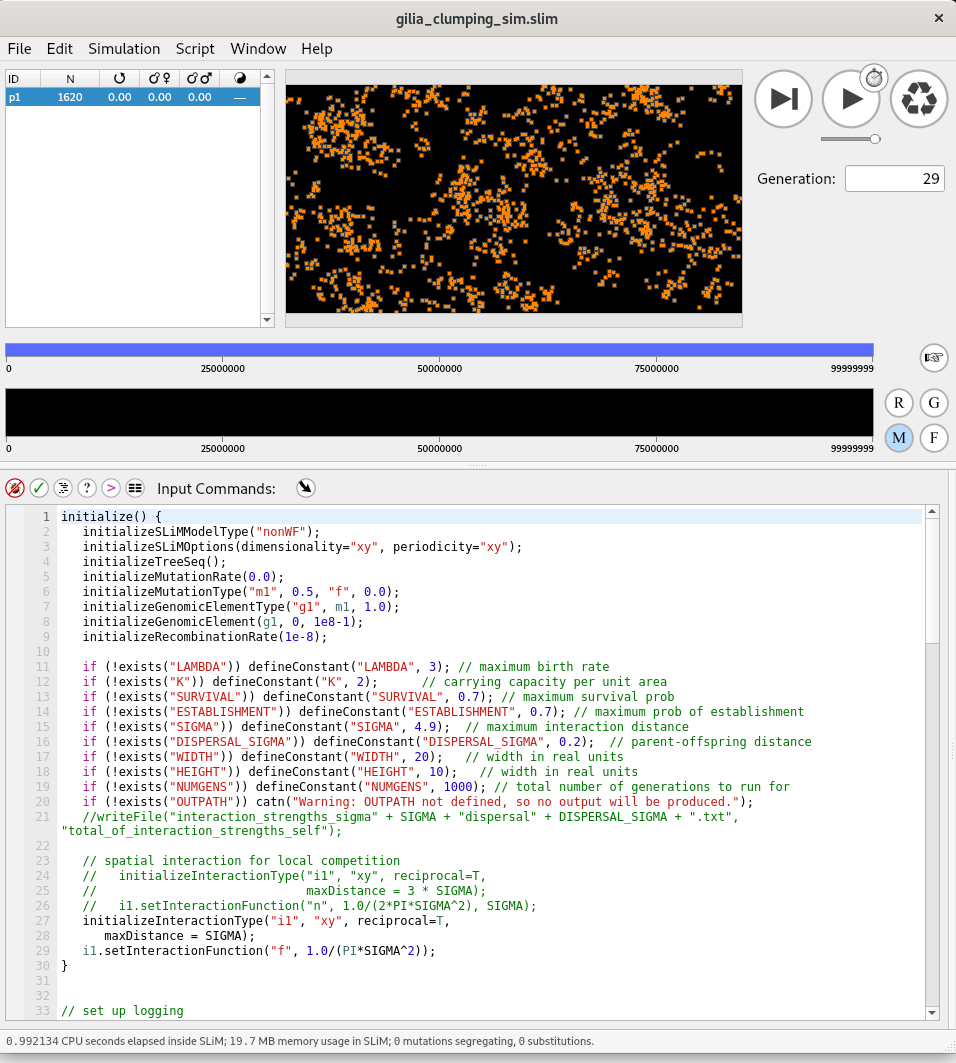
SLiM code at github.com/petrelharp/cirm_2021_talk
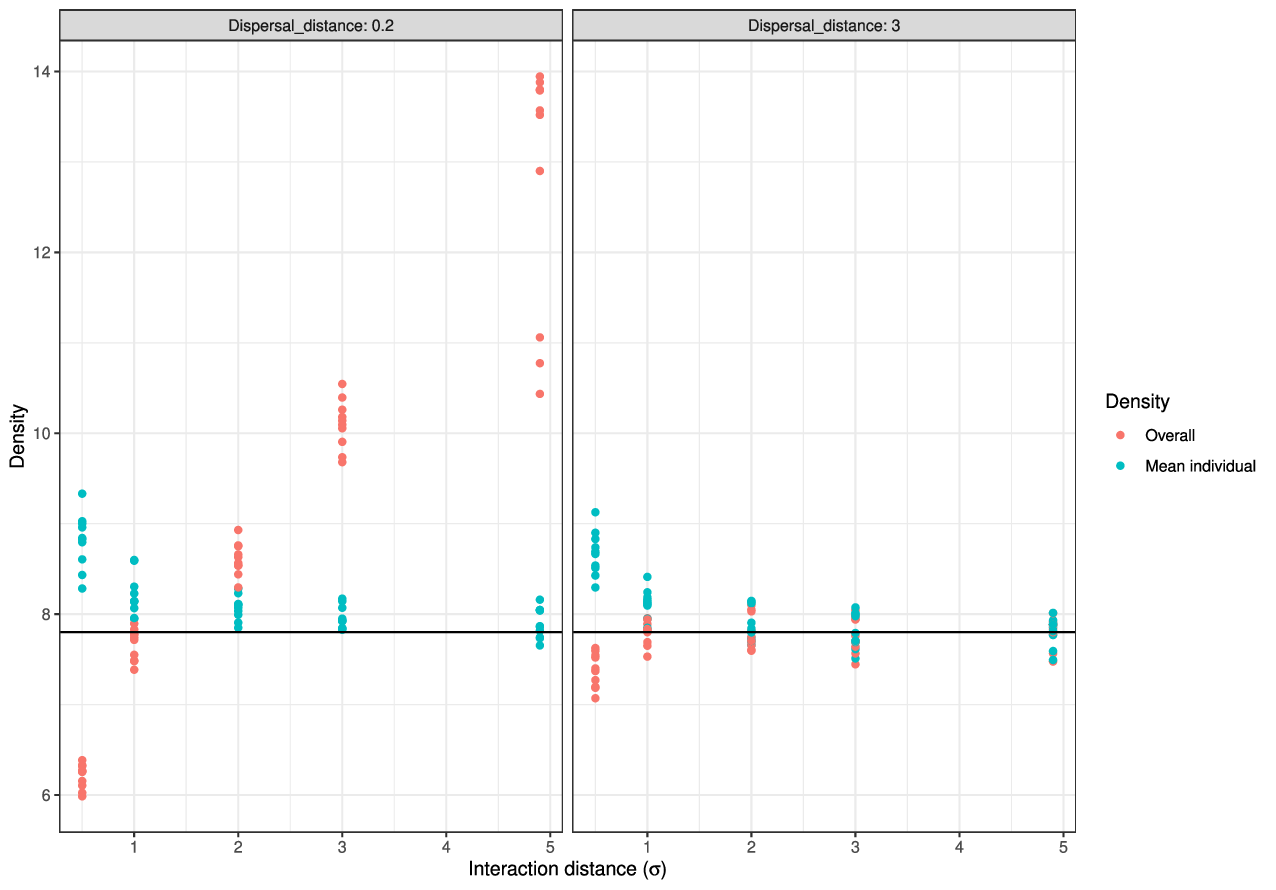
- dispersal distance \(\sigma = 1/\sqrt{\theta} = 3\)
- interaction distance \(\epsilon = 1\)
- mean # offspring \(\gamma \propto (1 + \text{(density)} / K)^{-1}\)
- dispersal distance \(\sigma = 1/\sqrt{\theta} = 0.2\)
- interaction distance \(\epsilon = 1\)
- mean # offspring \(\gamma \propto (1 + \text{(density)} / K)^{-1}\)
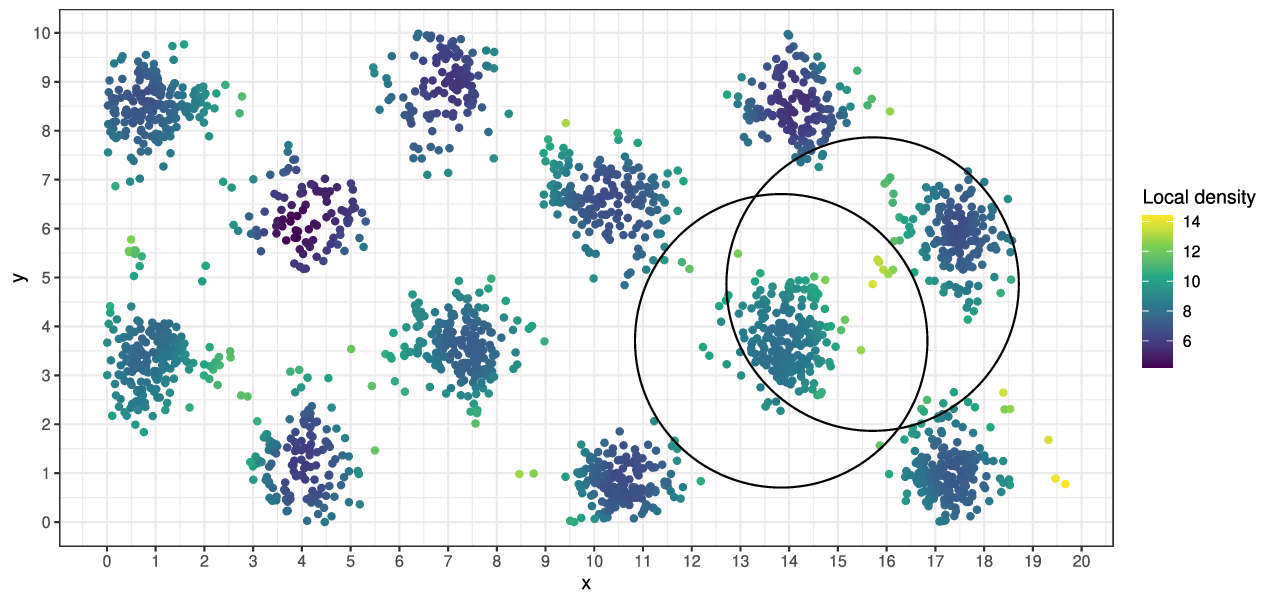
Consequences for stationary landscapes
If a deterministic, local limit holds, with dispersal \(N(m, \sigma^2 I)\), lineages should move in a stationary population density \(n(x) = d\Xi/dx\) as \[\begin{aligned} dL_t = r(L_t) \gamma(L_t) \left\{ \left( 2\sigma^2 \nabla \log(n\gamma)(L_t) - m \right) dt + \sigma dB_t \right\} . \end{aligned}\]
i.e., as Brownian motion run at speed \(\sigma r(y) \gamma(y)\) in the potential \[\begin{aligned} n(y) \gamma(y) e^{-my/(2\sigma^2)} , \end{aligned}\] … which has stationary distribution \[\begin{aligned} \frac{n(y)}{r(y)} e^{-my/(2\sigma^2)} . \end{aligned}\]
Lineages in expanding populations
Travelling waves
Suppose the population density has a traveling wave profile: \(\Xi_t(dx) = n(t,x) dx\) with \[\begin{aligned} n(x,t) = w(x - ct), \end{aligned}\] and a determinstic, local limit holds:
… then \(L + ct\) has generator \[\begin{aligned} \phi &\mapsto r(x) \gamma(x) \left\{ 2 \nabla \log(\gamma w)(x) \cdot \nabla \phi(x) + \Delta \phi(x) \right\} \\ &\qquad {} + c \cdot \nabla \phi(x) . \end{aligned}\]
Example: PME
For instance, take the porous medium equation with logistic growth (in 1D): \[\begin{aligned} \partial_t n_t(x) = \partial_x^2 [n_t(x)^2] + n_t(x) (1 - n_t(x)) , \end{aligned}\] with stable solution \[\begin{aligned} n_t(x) = \left( 1 - \exp\left( \frac{1}{2} (x - t) \right)\right)_+ \end{aligned}\]
To get this, we want \(r=1\) and \[\begin{aligned} \gamma(x, n) &= n(x) \\ \mu(x, n) &= 2 n(x) - 1 . \end{aligned}\]
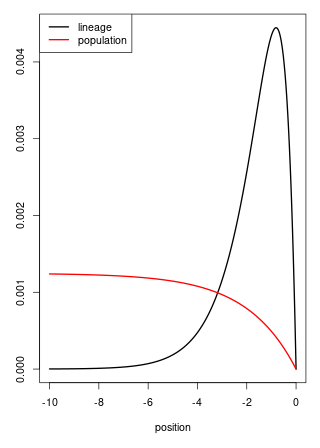
…so in the stationary frame, the lineage’s generator is \[\begin{aligned} \phi &\mapsto w(x) \left( \phi_{xx} + 4 (\log w)_x \phi_x \right) + \phi_x \\ &= \left(1 - e^{x/2}\right) \phi_{xx} + \left(1 - 2 e^{x/2}\right) \phi_x \qquad \text{on } x < 0. \end{aligned}\]
The lineage has stationary distribution \[\begin{aligned} \pi(x) \propto e^x \left(1 - e^{x/2}\right) \end{aligned}\] for \(x < 0\).
… in constrast to the Fisher-KPP.
Wrap-up
Open questions
When is \(\sigma_e > \sigma\)?
How badly are lineages non-Markov?
What can (and can’t) inferences about reverse-time tell us about forwards-time?
image by CJ Battey
Credit
- Alison Etheridge
- Tom Kurtz
- Ian Letter
- Terence Tsui
- Aaron Smith
- Gilia Patterson
and
- Andy Kern
- CJ Battey
- Gideon Bradburd
- the Kern-Ralph co-lab
Simulation methods:
- Ben Haller (messerlab.org/SLiM)
- Jerome Kelleher (tskit.dev/msprime)
- the tskit consortium (tskit.dev)