\[ \newcommand{\E}{\mathbb{E}} \renewcommand{\P}{\mathbb{P}} \DeclareMathOperator{\var}{var} \]

New tools for popgen simulation and analysis:
What’s possible?

Peter Ralph
University of Oregon
Institute of Ecology and Evolution

Evolution 2021
slides: github:petrelharp/evolution_2021

Overview of simulators

In this talk:

  • msprime: a coalescent simulator
  • SLiM: a forwards simulator

Other good ones:

msprime logo
SLiM logo

Forwards or backwards?

Forwards or backwards?

Do your digital organisms:

  • have at most one site under selection?
  • live in a collection of randomly-mating populations?
  • not need some specific life cycle?

If so, then coalescent simulation is the way to go!

msprime

msprime logo
jerome kelleher

Kelleher, Etheridge, & McVean 2016

msprime v1.0

msprime collaborators

New features:

  • \(k\)-ploid individuals, finite sites
  • recombination rate maps
  • gene conversion
  • nicer demographic model specification
  • mutation rate maps
  • quick analysis

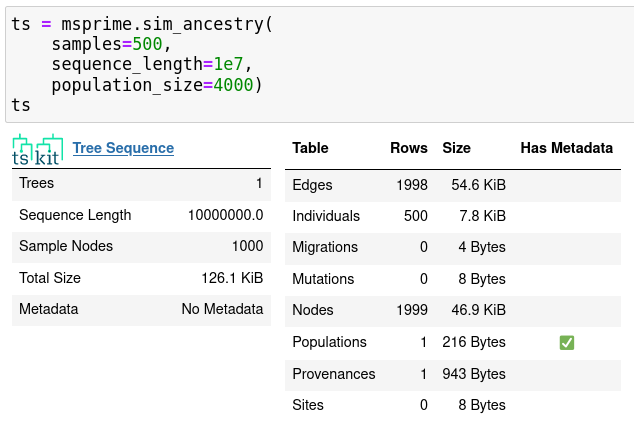
New features:

  • \(k\)-ploid individuals, finite sites
  • recombination rate maps
  • gene conversion
  • nicer demographic model specification
  • mutation rate maps
  • quick analysis

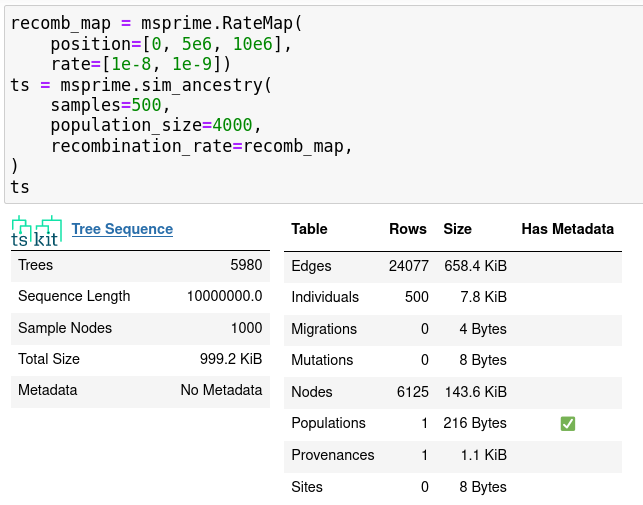
New features:

  • \(k\)-ploid individuals, finite sites
  • recombination rate maps
  • gene conversion
  • nicer demographic model specification
  • mutation rate maps
  • quick analysis

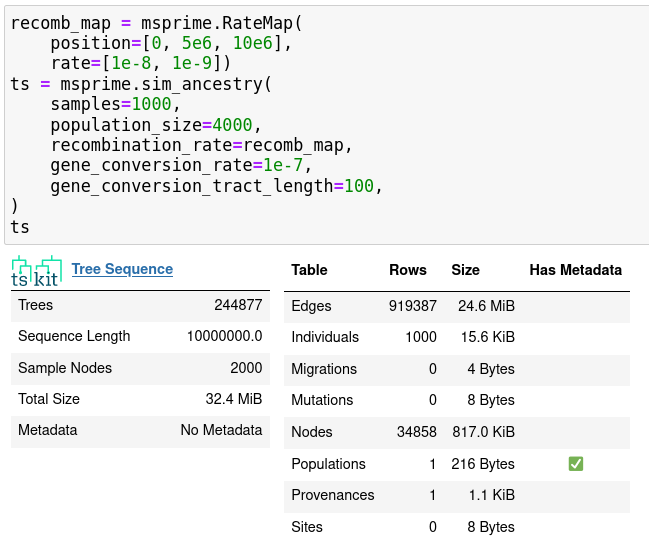
New features:

  • \(k\)-ploid individuals, finite sites
  • recombination rate maps
  • gene conversion
  • nicer demographic model specification
  • mutation rate maps
  • quick analysis

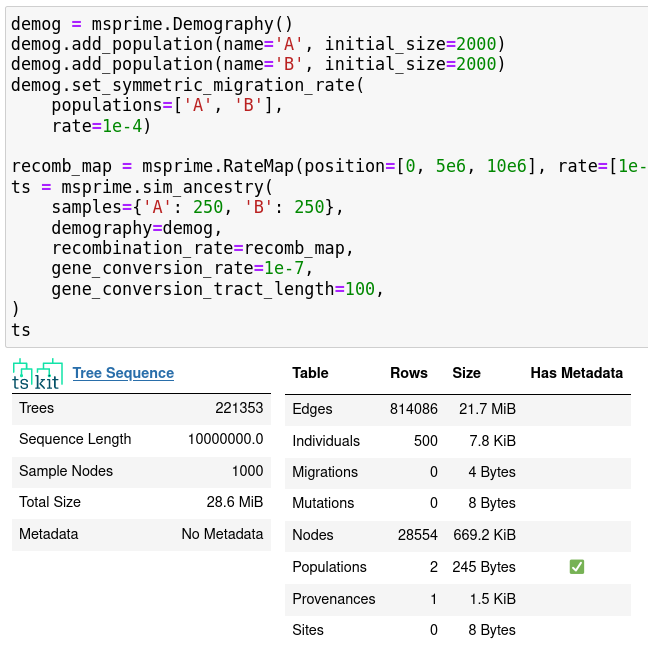
New features:

  • \(k\)-ploid individuals, finite sites
  • recombination rate maps
  • gene conversion
  • nicer demographic model specification
  • mutation rate maps
  • quick analysis

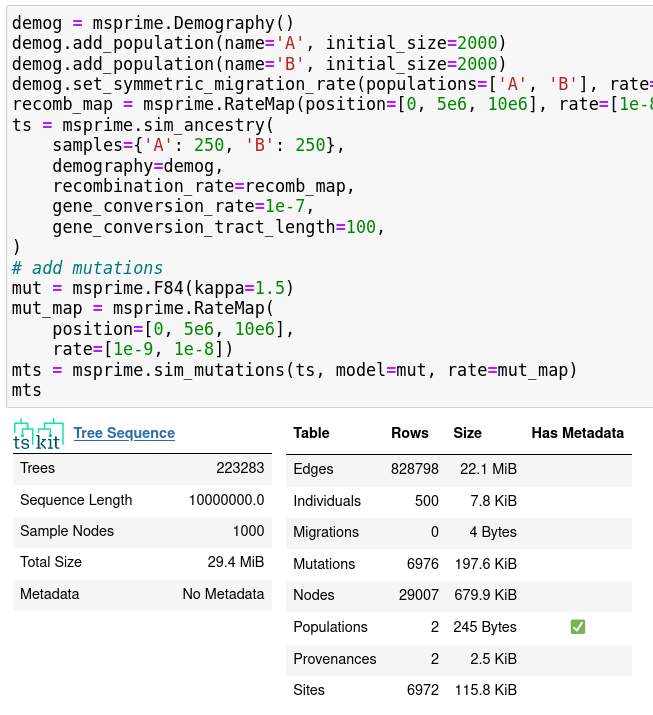
New features:

  • \(k\)-ploid individuals, finite sites
  • recombination rate maps
  • gene conversion
  • nicer demographic model specification
  • mutation rate maps
  • quick analysis

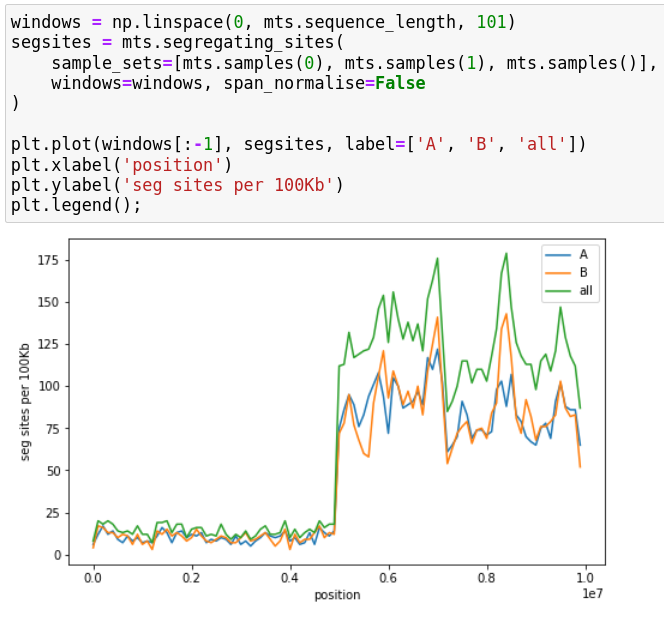
Ancestry models

  • “the” coalescent
  • discrete-time Wright-Fisher
  • multiple mergers
  • selective sweeps
sweep_model = msprime.SweepGenicSelection(
    position=2.5e4, s=0.01,
    start_frequency=0.5e-4, end_frequency=0.99, dt=1e-6)
sts = msprime.sim_ancestry(9,
    model=[sweep_model, msprime.StandardCoalescent()],
    population_size=1e4, recombination_rate=1e-8, sequence_length=5e4)

Mutation models

  • infinite sites/alleles
  • nucleotides
  • amino acids
  • arbitrary Markovian models
dem = msprime.Demography.from_species_tree(
   "((A:900,B:900)ab:100,C:1000)abc;",
   initial_size=1e3)
samples = {"A": 2, "B": 1, "C": 1}
ts = msprime.sim_ancestry(
   8, demography=dem, sequence_length=5e4,
   recombination_rate=1e-8
)
mts = msprime.sim_mutations(ts, rate=1e-7)
mts.draw_svg()

SLiMv3

An eco-evolutionary simulator

  • everything msprime can
  • ecological dynamics with “non-Wright-Fisher” models
  • populations in continuous, heterogeneous geography
  • sex chromosomes, haplodiploidy
  • complex traits
  • context-dependent mutations
  • v4: interacting species
SLiM logo
Ben Haller

Ben Haller

Getting started:

  1. read the introduction of the SLiM manual
  2. find a recipe that’s close to what you want
  3. open up the GUI and try it
  4. print stuff in the console
  5. add in other bits
  6. take a workshop!

tree sequences

tskit logo
jerome kelleher

Kelleher, Etheridge, & McVean 2016

tskit contributors

Development philosophy

  • open, welcoming, supportive
  • well-documented
  • reliable, reproducible
  • backwards compatible
tskit logo

tskit: the tree sequence toolkit

https://tskit.dev

The tree sequence

video credit: Yan Wong

Benefits

  • extremely efficient for large simulations
  • retains genotypes and genealogical history

Interoperable: now supported by

Post-hoc mutations

diagram of adding mutations to a tree sequence

Recapitation

diagram of recapitation

Runtime

  • \(N_e\) = population size
  • \(L\) = genome length
  • \(T\) = # of generations
  • sample size doesn’t matter
  • “chromosome” = \(10^8\) bp

  • msprime: quadratic in \(N_e L\)

    • chromosomes, \(N_e = 1,000\): seconds
    • megabases, \(N_e = 100,000\): seconds
    • chromosomes, \(N_e = 100,000\): hours
    • megabases, \(N_e = 10,000,000\): hours

  • SLiM: linear in \(N_e T\)

    • \(N_e = 1,000\): seconds/thousand gens
    • \(N_e = 100,000\): minutes/thousand gens
    • selection: 3x slower
    • space: 10x slower with neighborhood size 20

How long do I run it for?

  1. Until equilibrium. (4N? 20N?)
  2. If that’s too long, for a “while”, and recapitate.
  3. Your results shouldn’t depend too much on how you do it.

Big picture: how accurate do you think your demographic model reflects 2N generations ago, really?

Considerations

  • \(N\) = population size
  • \(L\) = genome length
  • sample size (doesn’t matter much)
  • number of generations (SLiM only)
  • selection
  • geography
  • adding neutral mutations (nearly instant)

msprime: 1000 samples

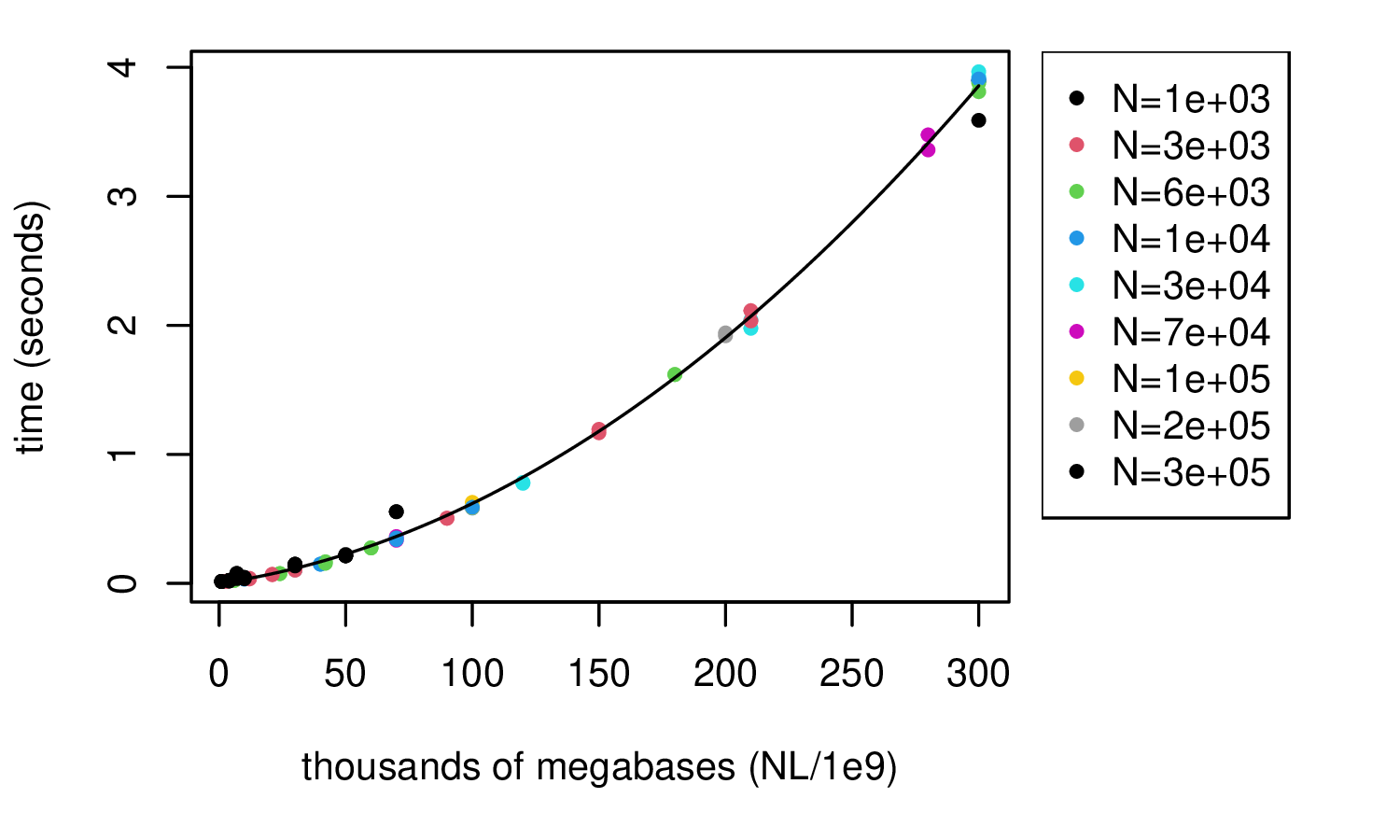
takeaway: hundreds of thousands of megabases takes seconds

msprime: 1000 samples

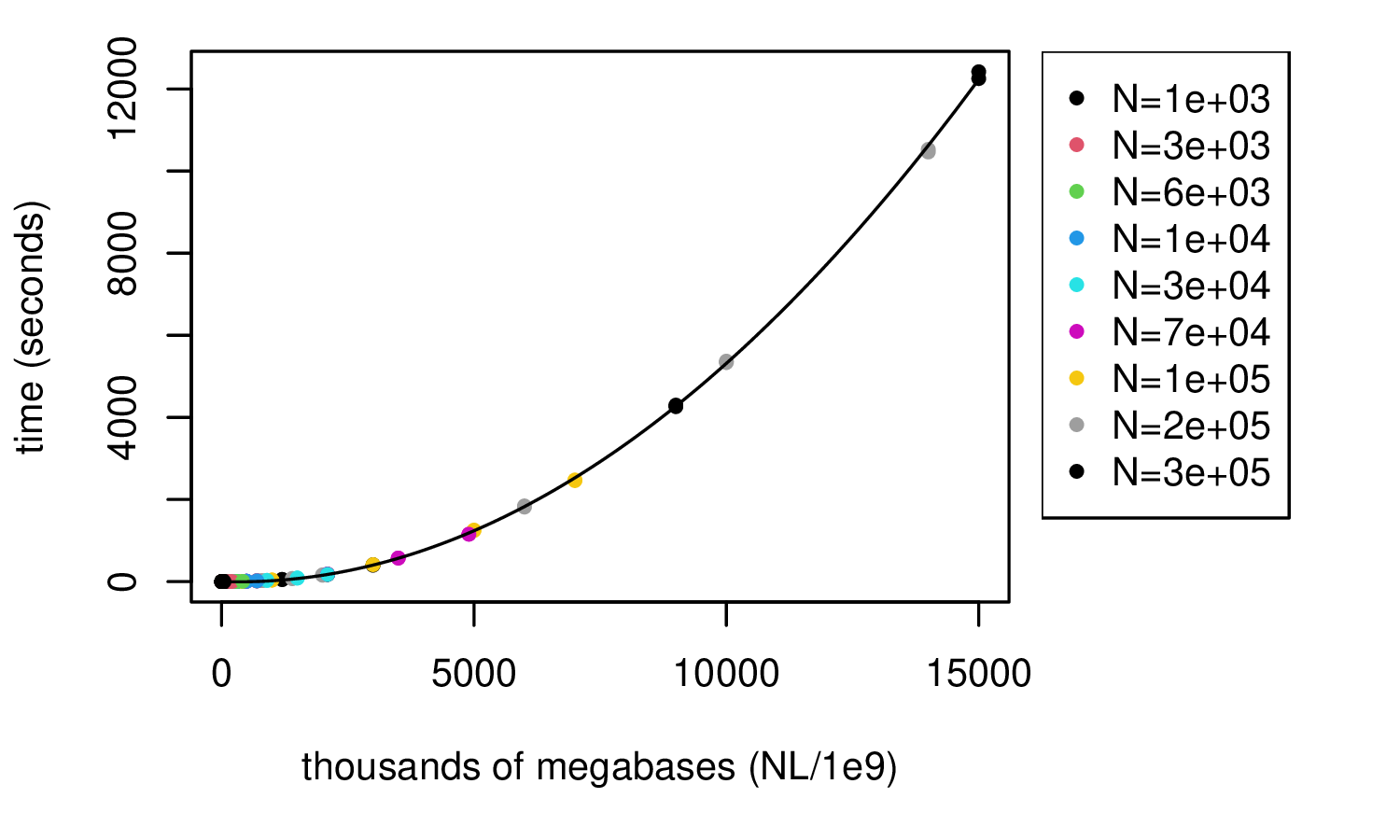
takeaway: hundreds of thousands of megabases takes seconds

basic demography: SLiM

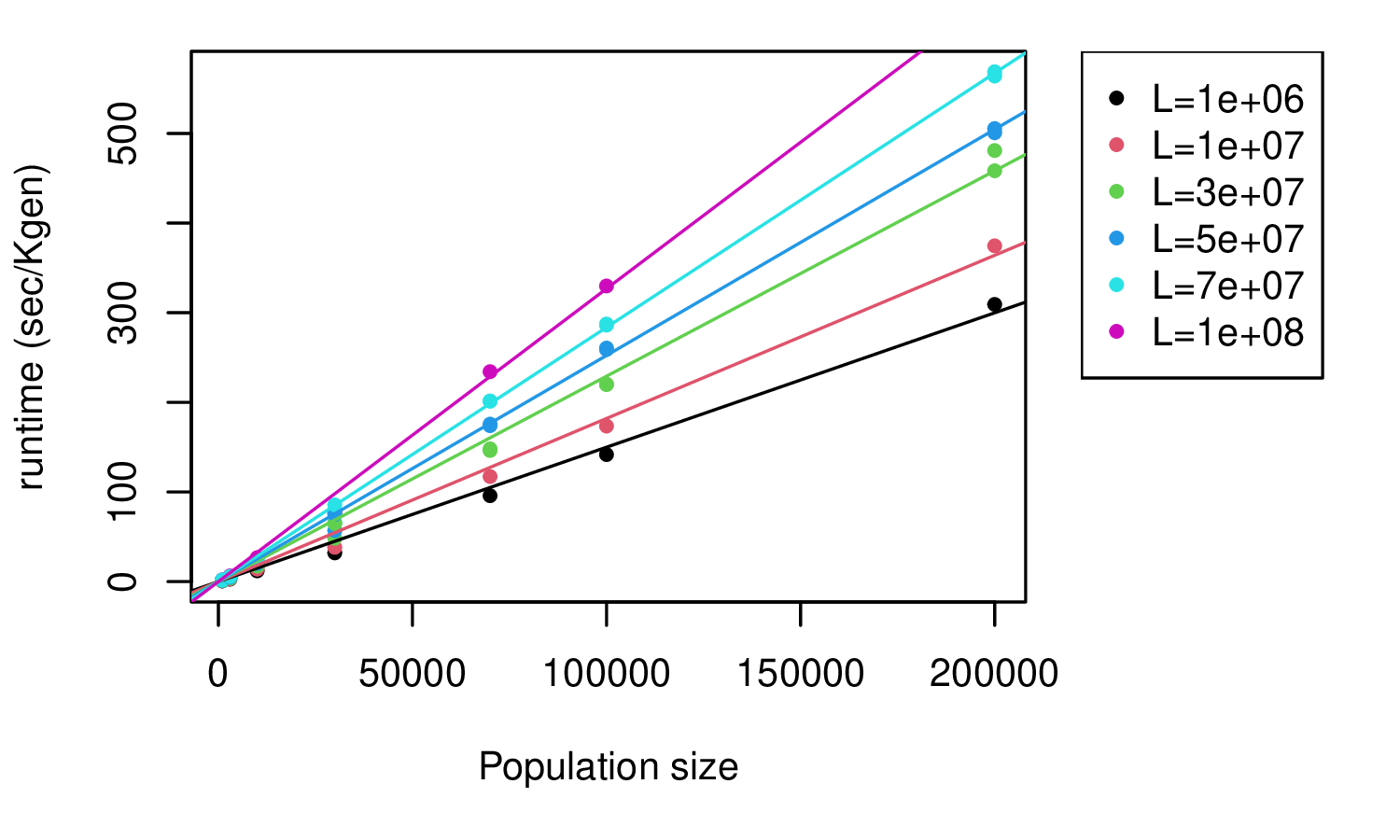
takeaway: linear in population size

Basic demography: SLiM

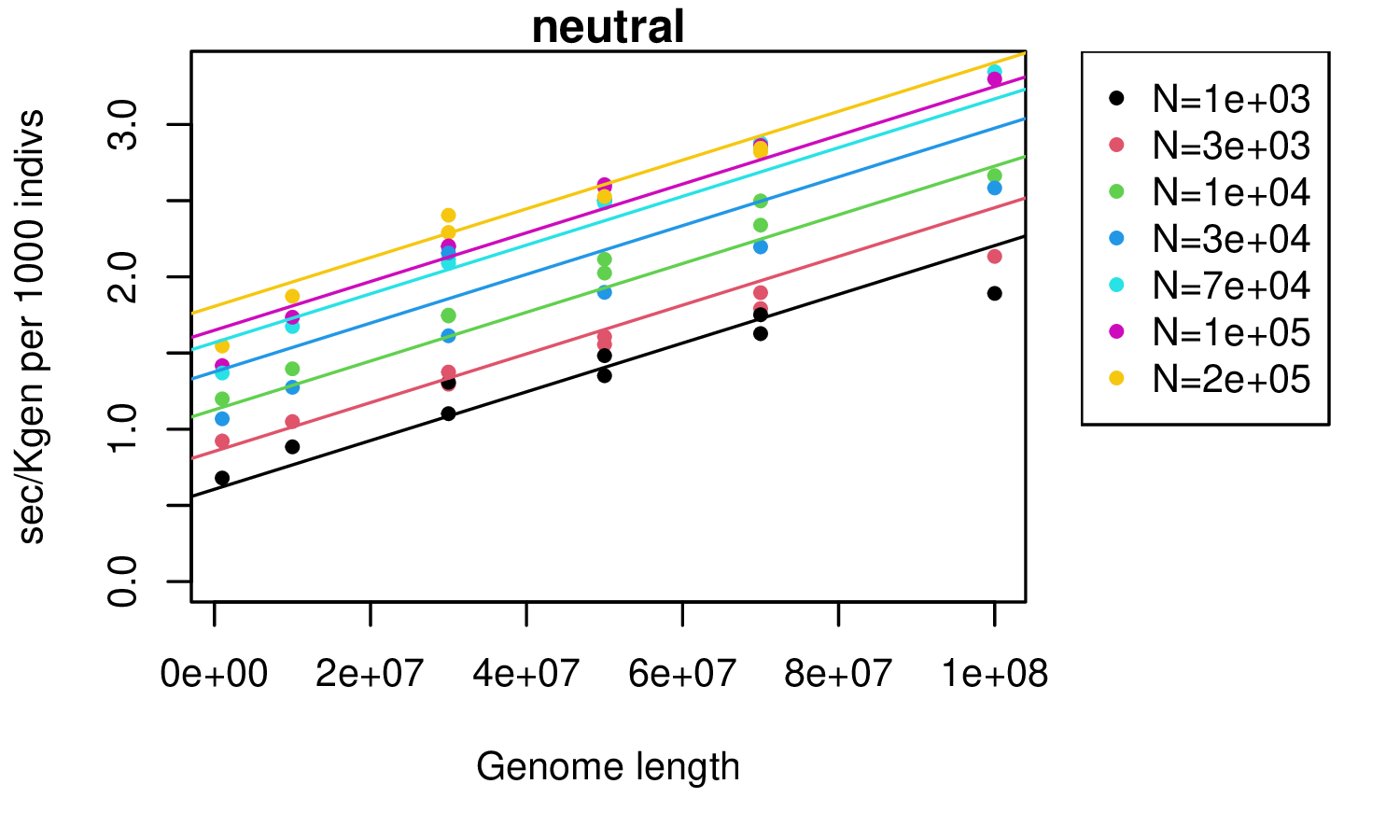
takeaway: seconds per thousand individuals per thousand generations

Selection: SLiM, total rate \(10^{-10}\)

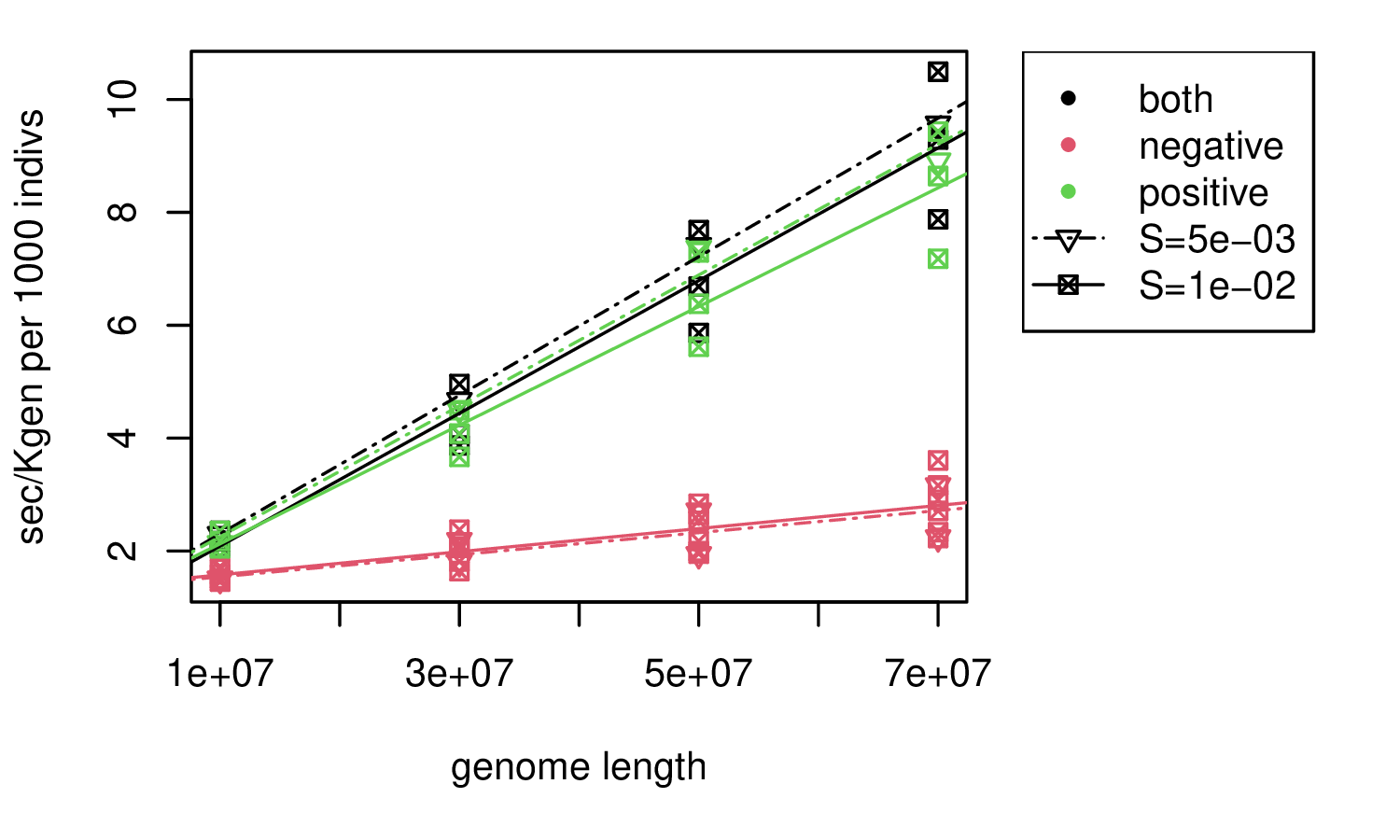
takeaway: similar, but slower by a factor of 3 for lots of positive mutations

Spatial simulations: SLiM

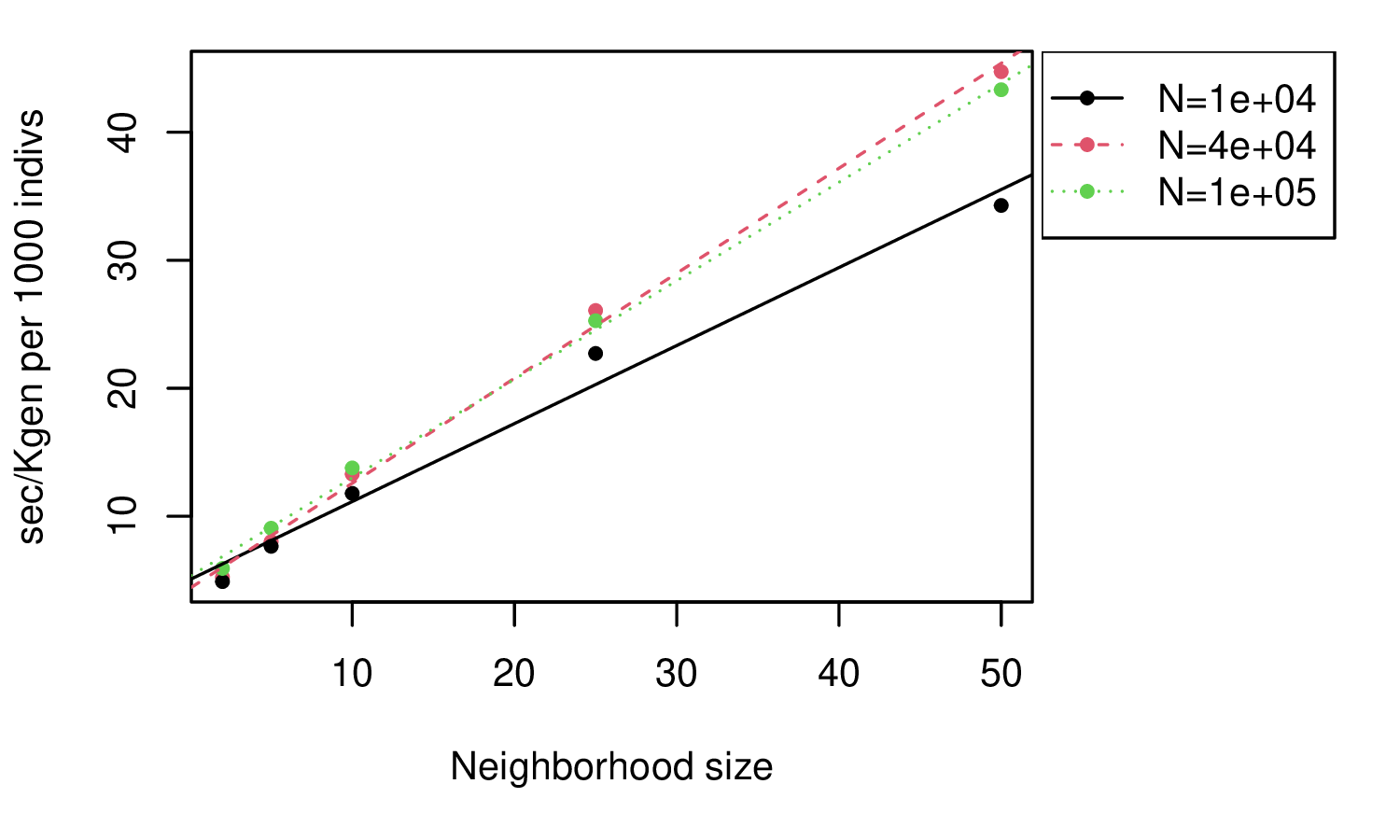
takeaway: 3x slower than genomes! Scales with neighborhood size (\(\sigma^2\)).

Thanks!

BDI
NHGRI
tskit logo
  • Jerome Kelleher
  • Ben Haller
  • Ben Jeffery
  • Yan Wong
  • Murillo Rodrigues
  • Andy Kern
  • Philipp Messer

https://tskit.dev/

How to get help

// reveal.js plugins