\[ \newcommand{\E}{\mathbb{E}} \renewcommand{\P}{\mathbb{P}} \DeclareMathOperator{\var}{var} \]

Landscapes in population genetics:

ecology, evolution, and simulation

Peter Ralph

University of Oregon // October 2019

Outline

Outline of the talk

  1. Big picture
  2. Tools
  3. Applications

Students/postdocs/researchers:

  • Matt Lukac
  • Murillo Rodrigues
  • Jared Galloway
  • Jaime Ashander
  • Josh Schiffman
  • Erik Lundgren
  • Han Li
  • Jessica Crisci

Funding:

  • NSF DBI
  • Sloan foundation
  • UO Data Science

Other collaborators:

  • CJ Battey
  • Gideon Bradburd
  • Yaniv Brandvain
  • Madeline Chase
  • Graham Coop
  • Bill Cresko
  • Matt Dean
  • Alison Etheridge
  • Ben Haller
  • Katja Kasimatis
  • Jerome Kelleher
  • Andy Kern
  • Evan McCartney-Melstad
  • Patrick Phillips
  • Alisa Sedghifar
  • Brad Shaffer
  • Sean Stankowski
  • Matt Streisfeld
  • Anastasia Teterina

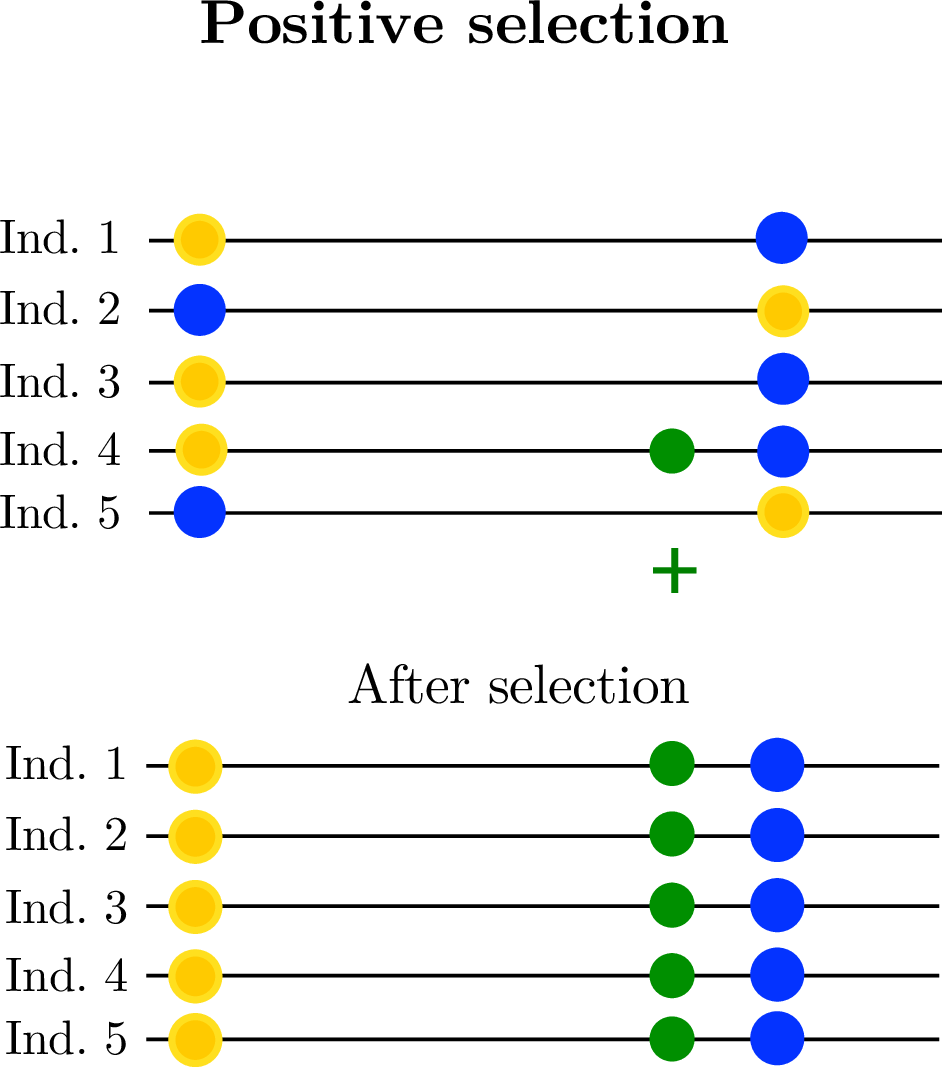
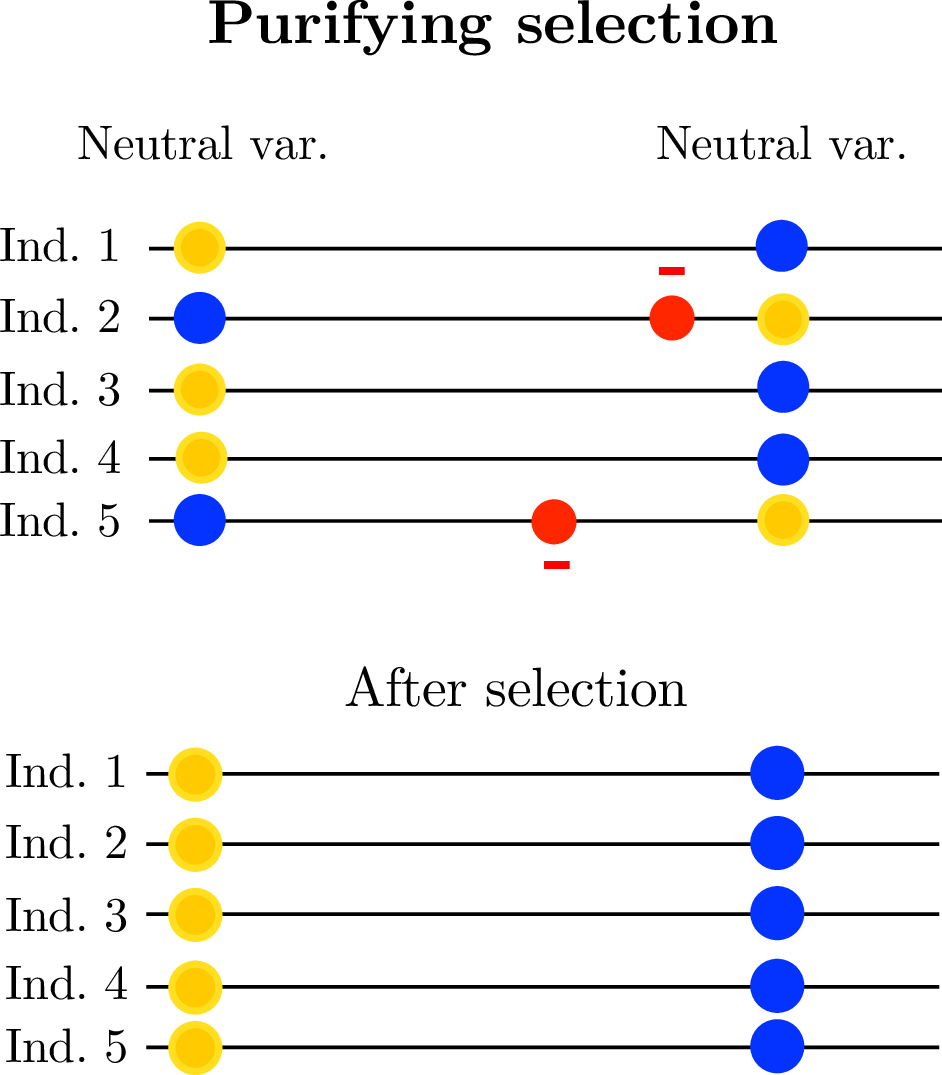
Adaptation, and genetic variation

Sickle-cell (HbS) allele frequencies

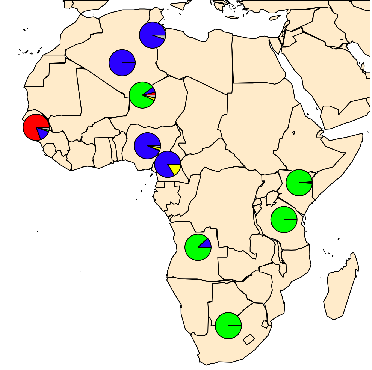
sickle-cell HbS allele map, from Flint et al 1998
sickle-cell HbS allele map, from Flint et al 1998

Human sickle-cell allele (HbS): (Currat et al 2002)

  • Single base substitution
  • provides protection against malaria (but deleterious in homozygotes)

G6PD deficiency allele frequencies

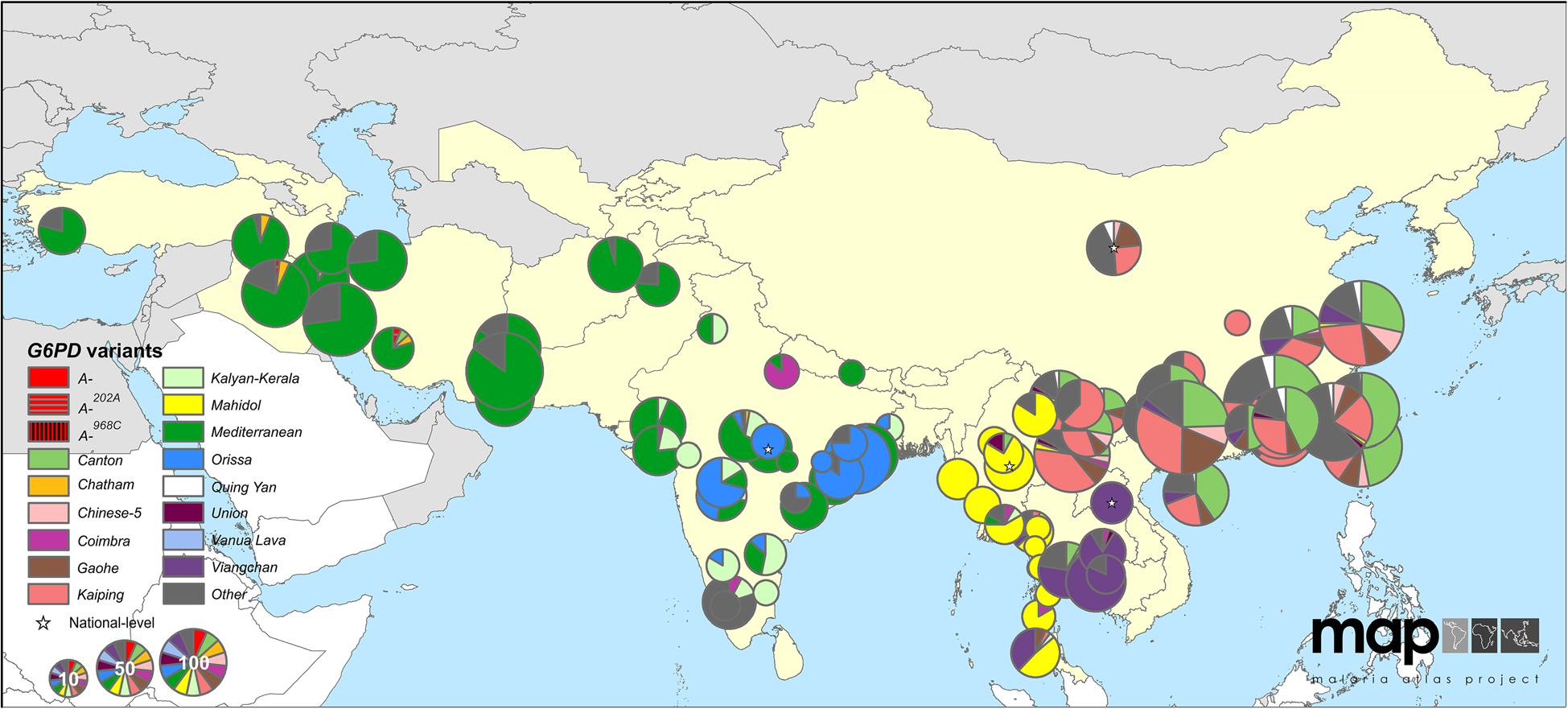
glucose-6-phosphate dehydrogenase deficiency alleles from Howes et al 2013
glucose-6-phosphate dehydrogenase deficiency alleles from Howes et al 2013

Human G6PD variants: Howes et al 2013)

  • over 130 G6PD deficiency alleles; 34 variants at high frequency
  • provide protection against malaria but increases risk of anemia
  • Estimated ages 40-400 generations

volcanic outcrops: mice by AH Harris
volcanic outcrops: mice by AH Harris
  • Dark-pigmented mammals and reptiles on volcanic outcrops in the Southwest. (Dice, Benson 1936)
  • ‘Dark’ allele beneficial on outcrops, deleterious elsewhere.
  • MC1R: basis is shared between species but not between populations (Nachman, Hoekstra)

How generalizable is this?

Genomic landscapes

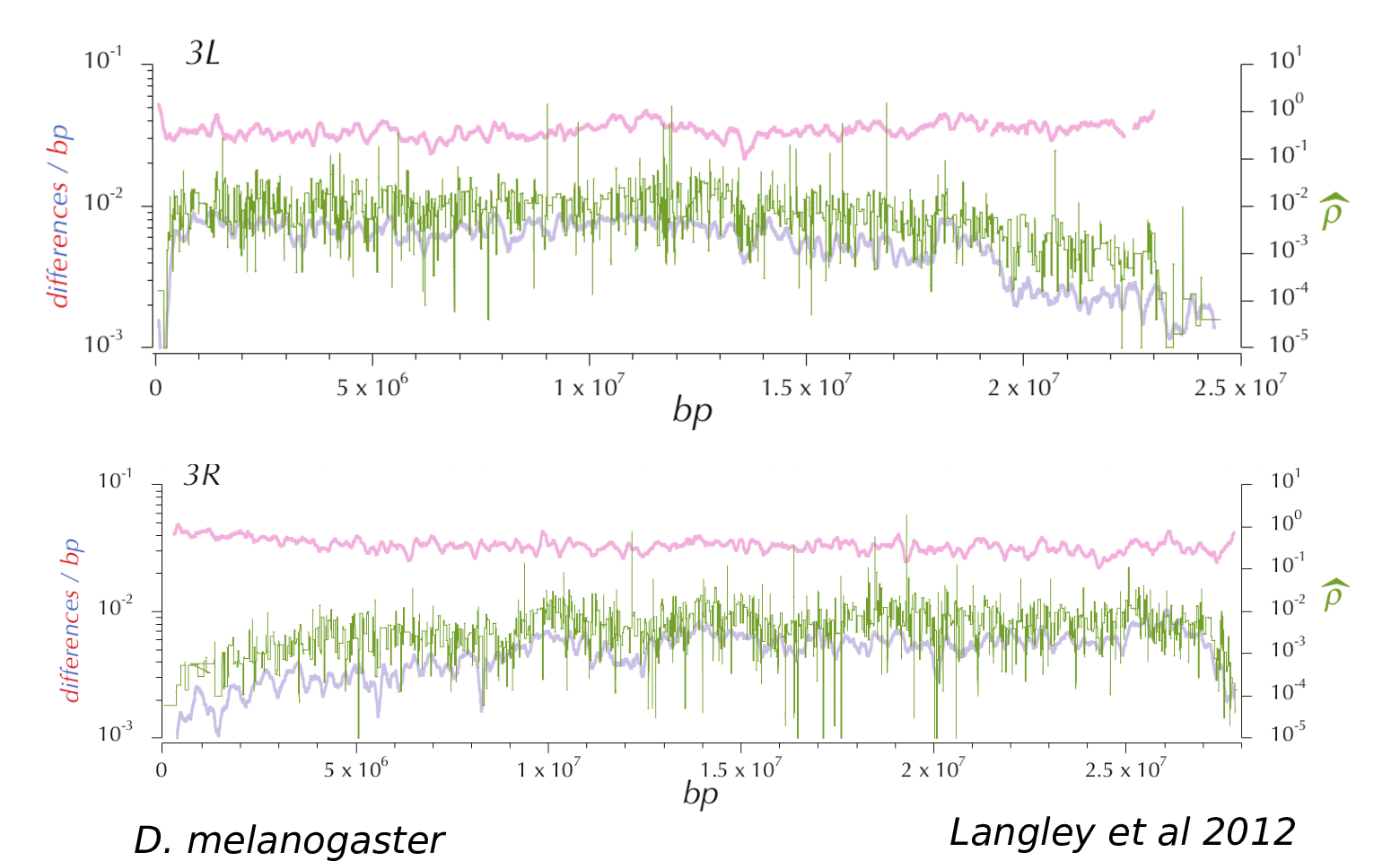
Langley et al 2012
Langley et al 2012

Diversity correlates with recombination rate

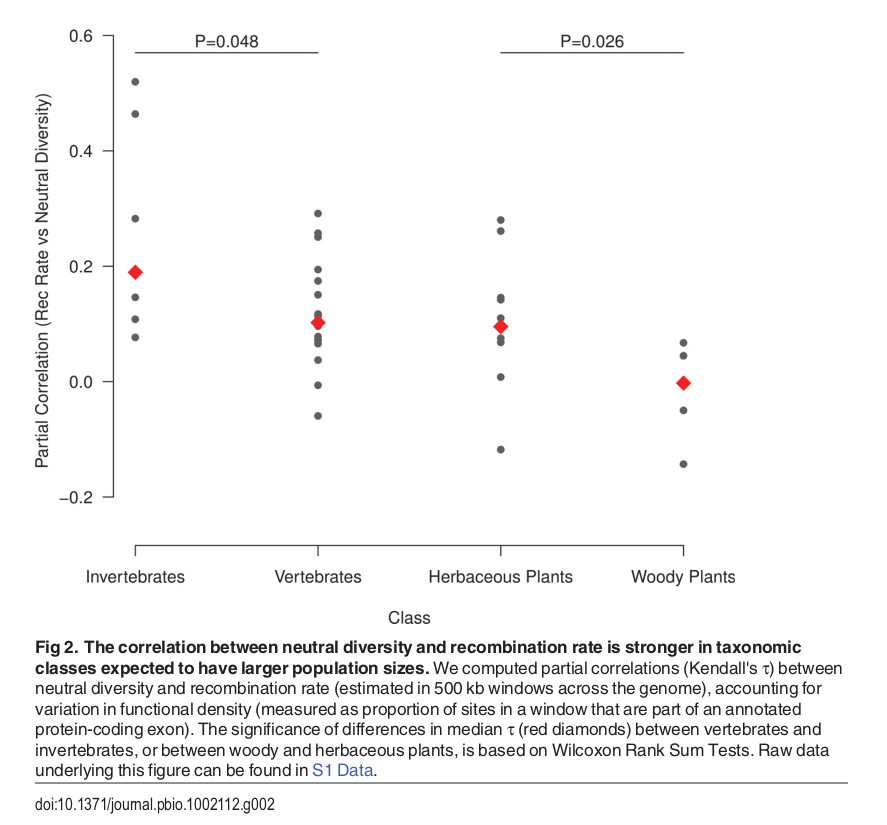
Corbett-Detig et al
Corbett-Detig et al

Hudson 1994; Cutter & Payseur 2013; Corbett-Detig et al 2015

linked selection

The indirect effects of selection on genomic locations that are linked to the sites under selection by a lack of recombination.

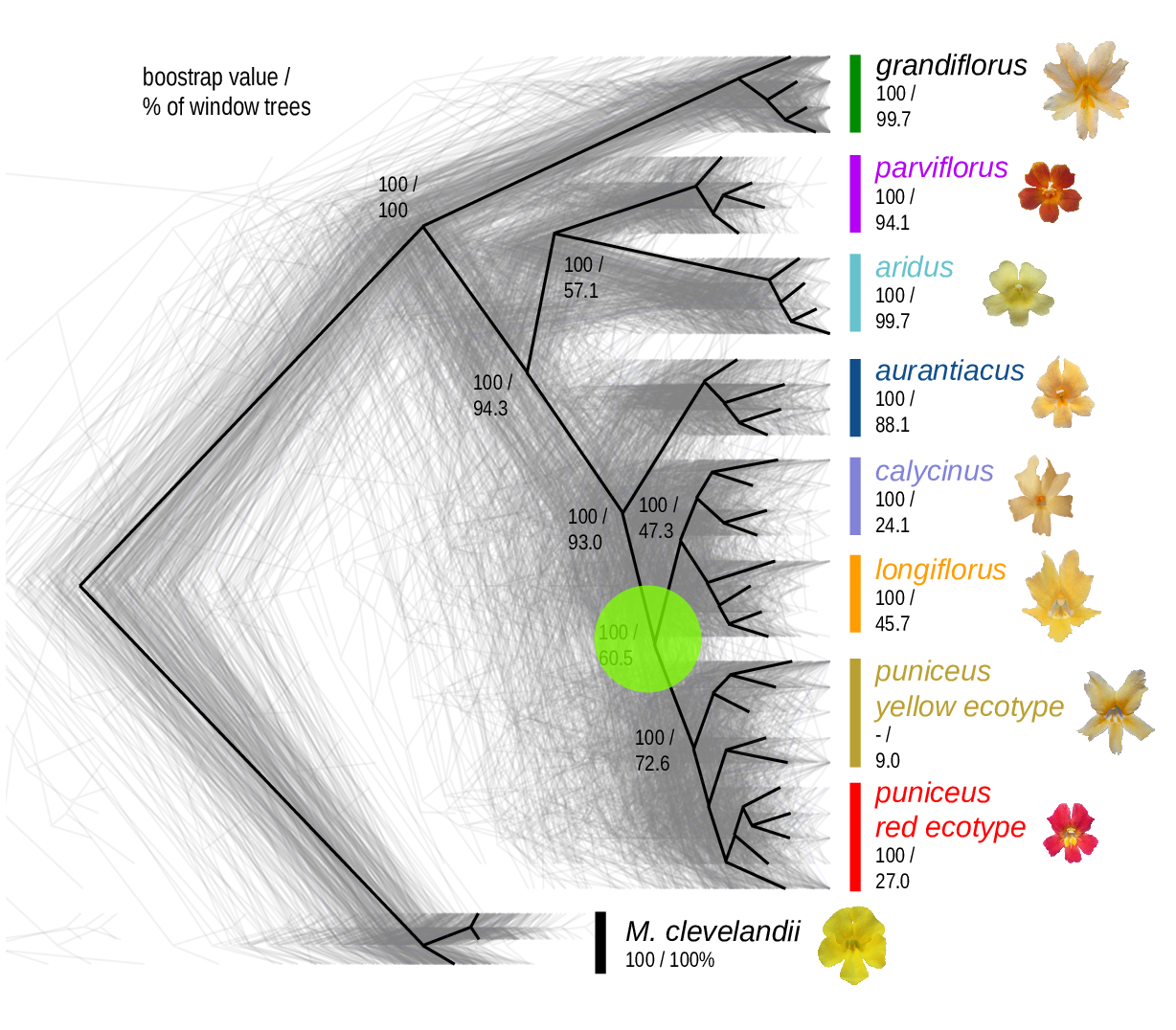
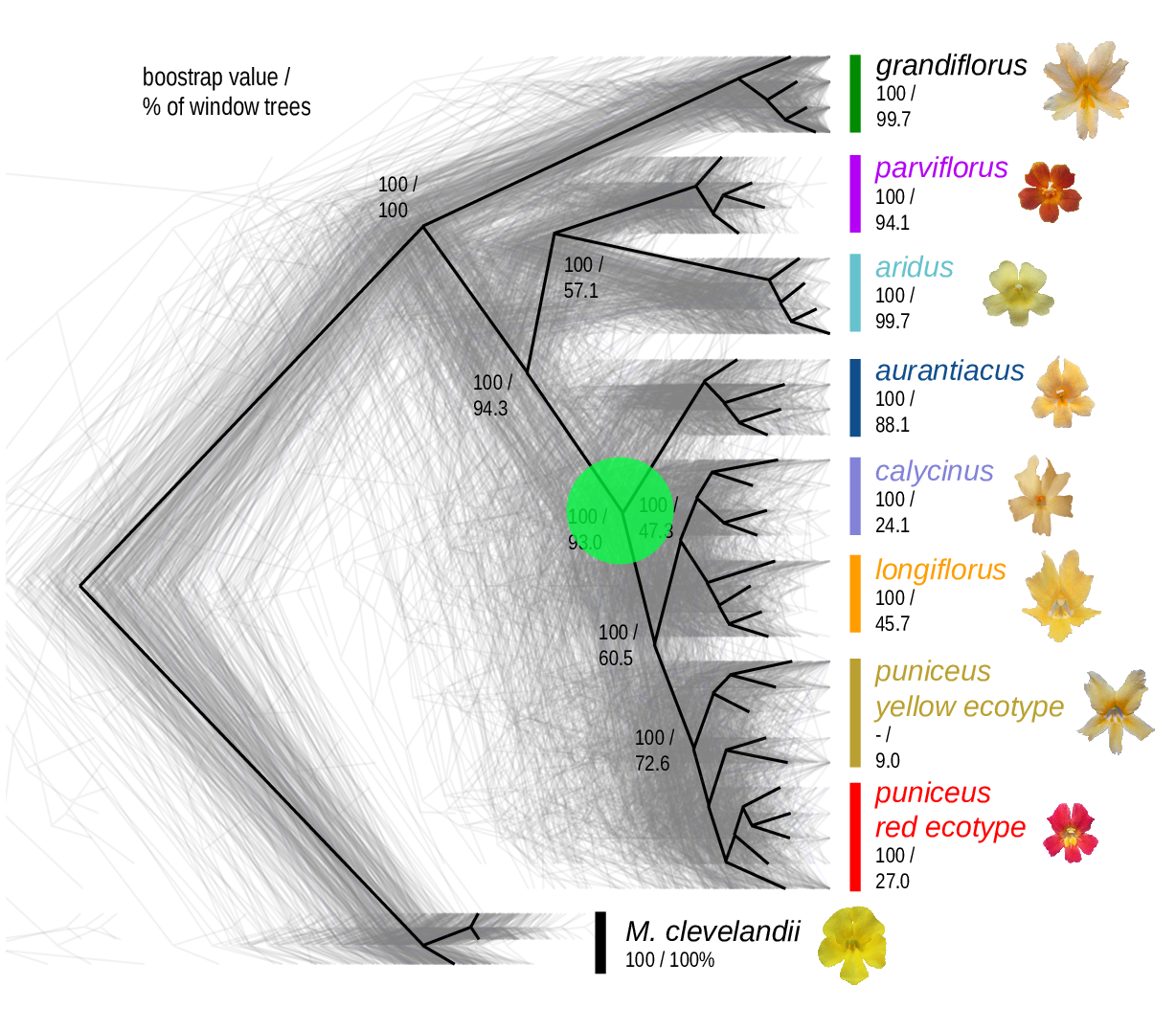
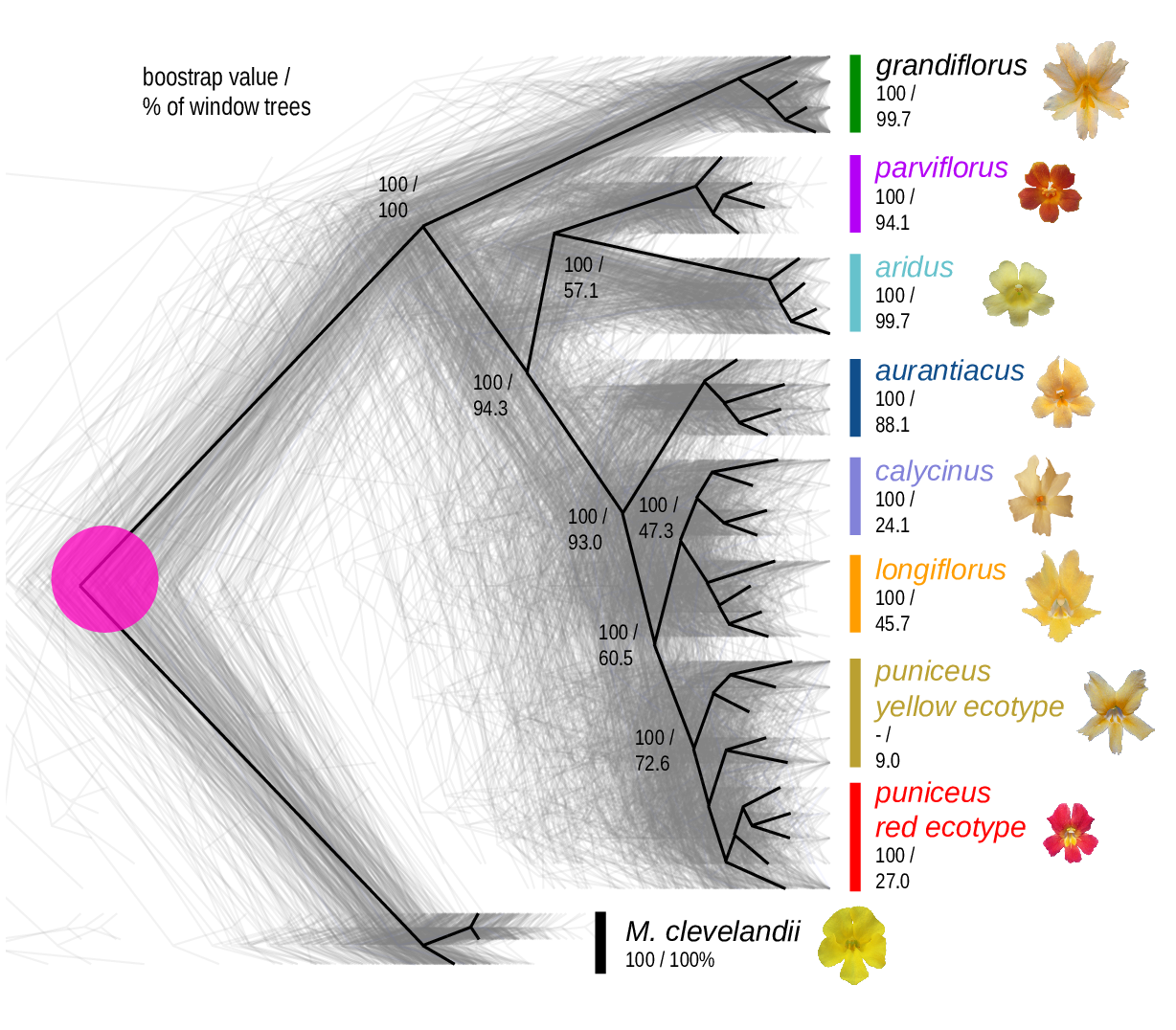
The Mimulus aurantiacus species complex

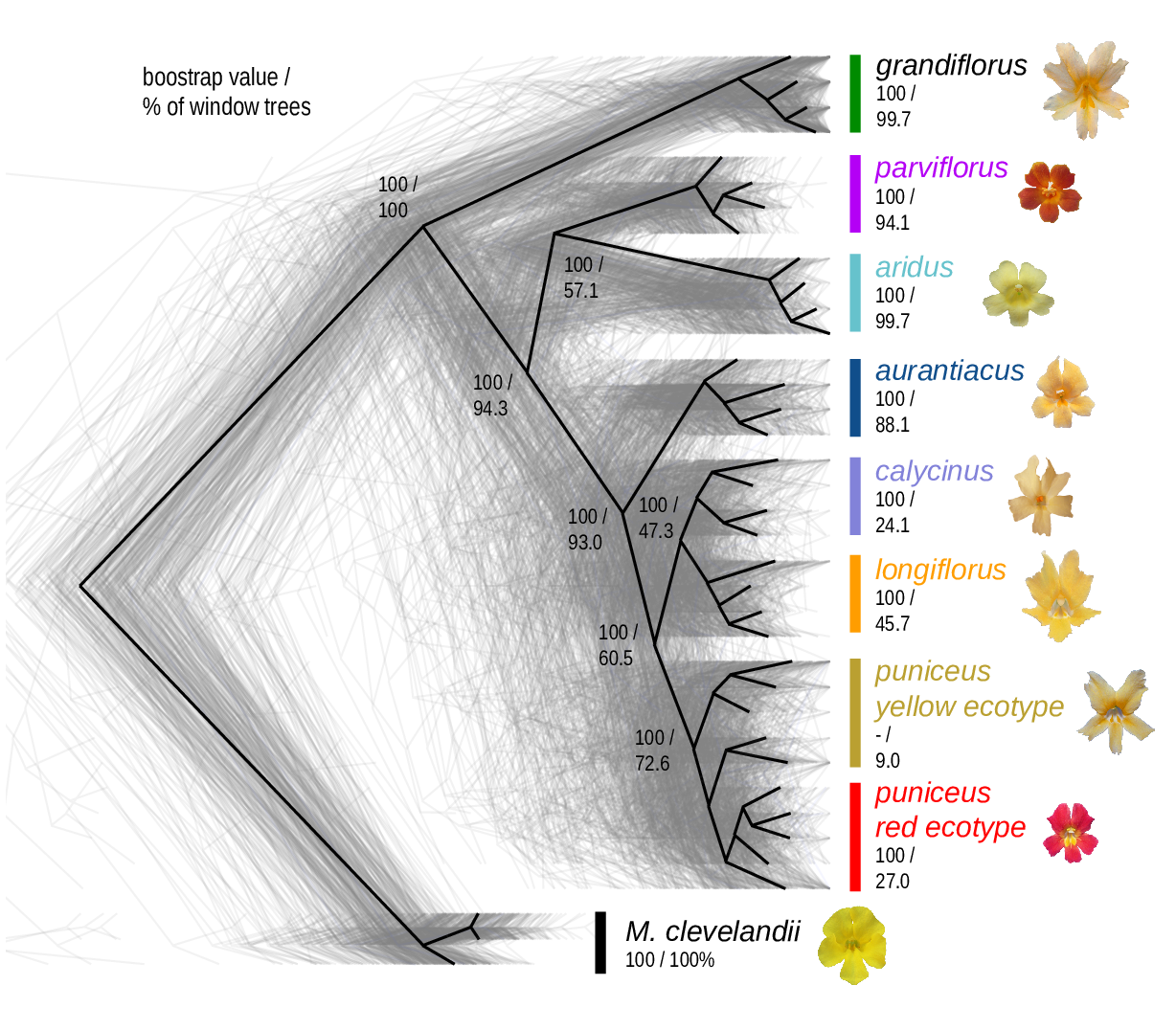
From Widespread selection and gene flow shape the genomic landscape during a radiation of monkeyflowers, Sean Stankowski, Madeline A. Chase, Allison M. Fuiten, Murillo F. Rodrigues, Peter L. Ralph, and Matthew A. Streisfeld; PLoS Bio 2019.

sean stankowski madeline chase matt streisfeld

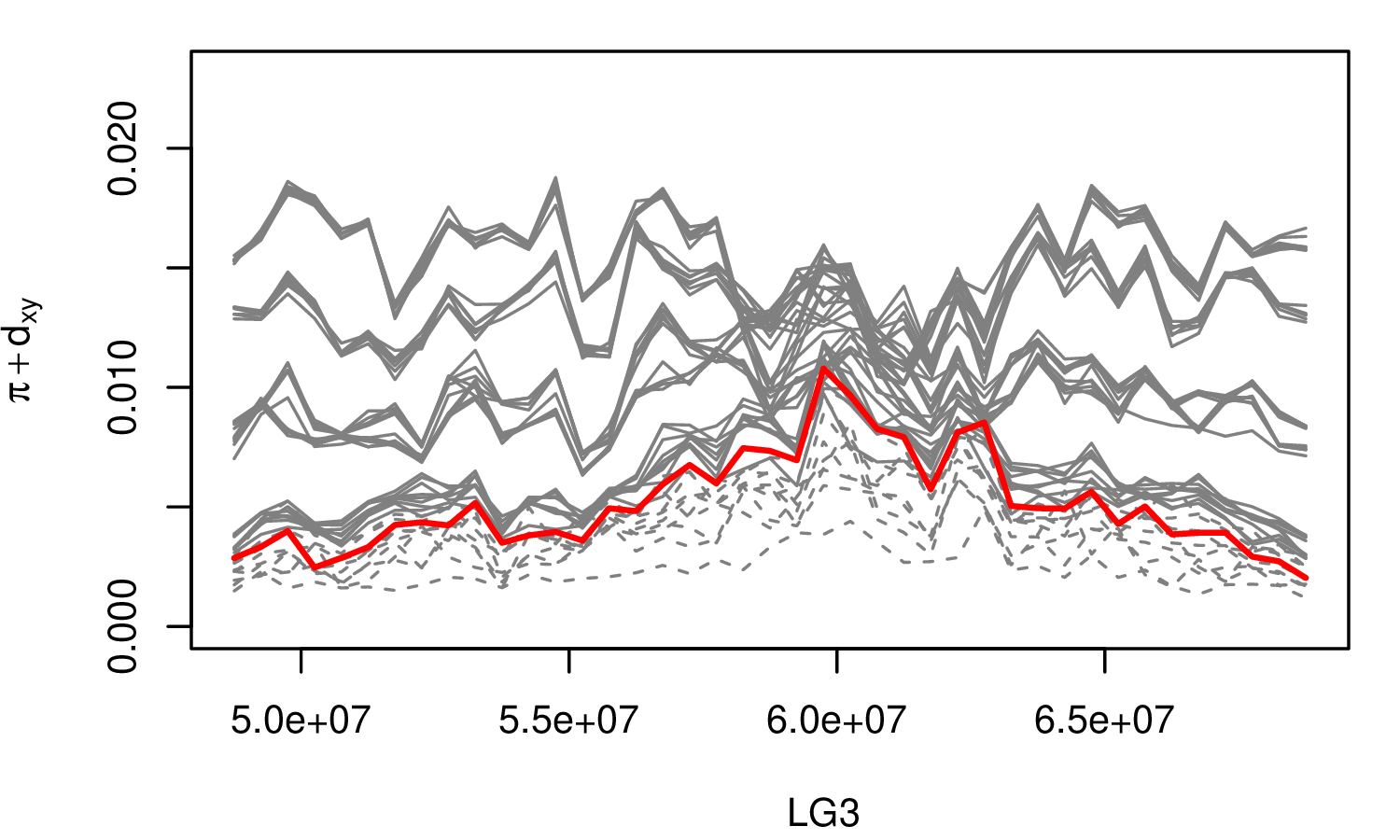
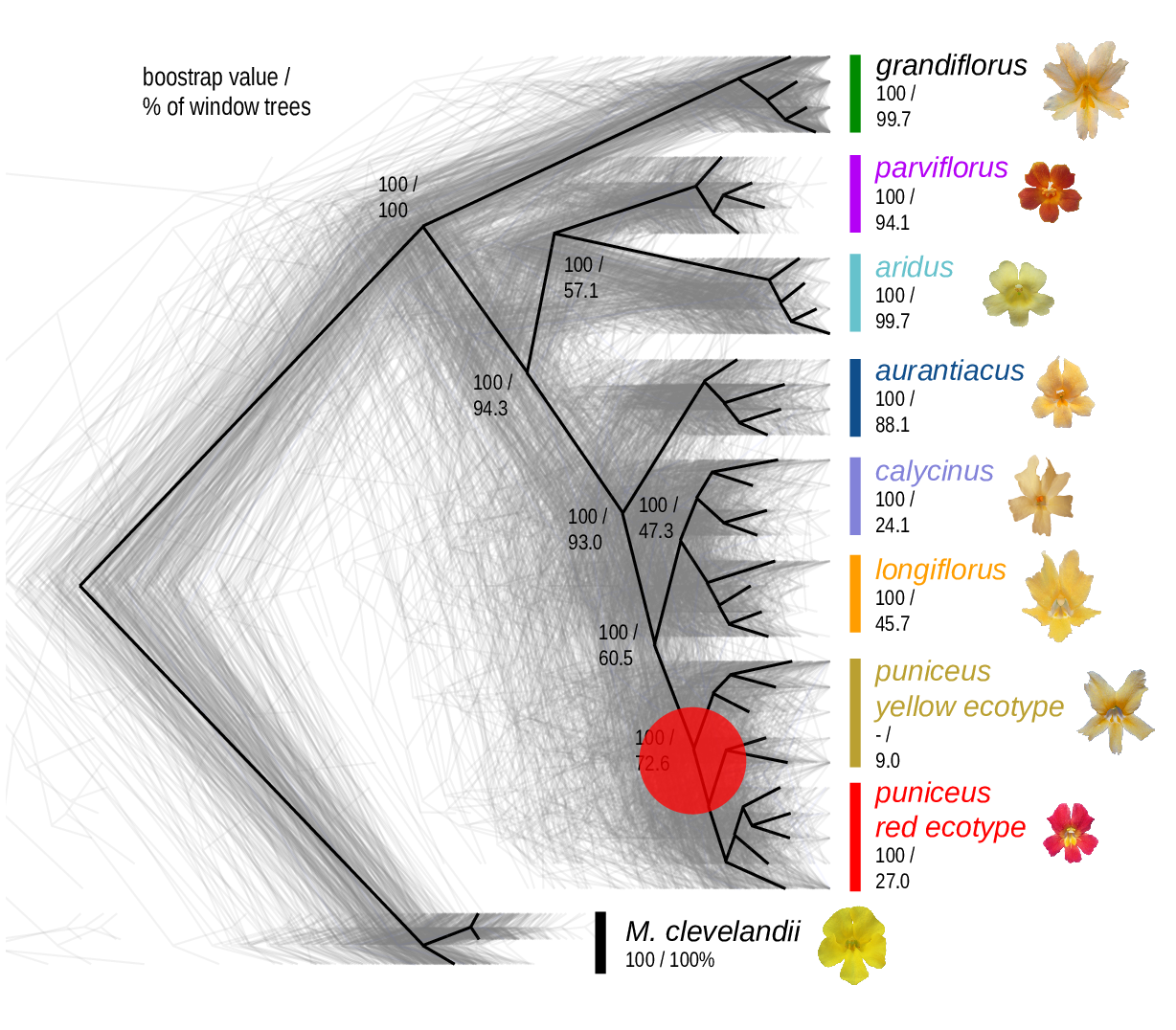
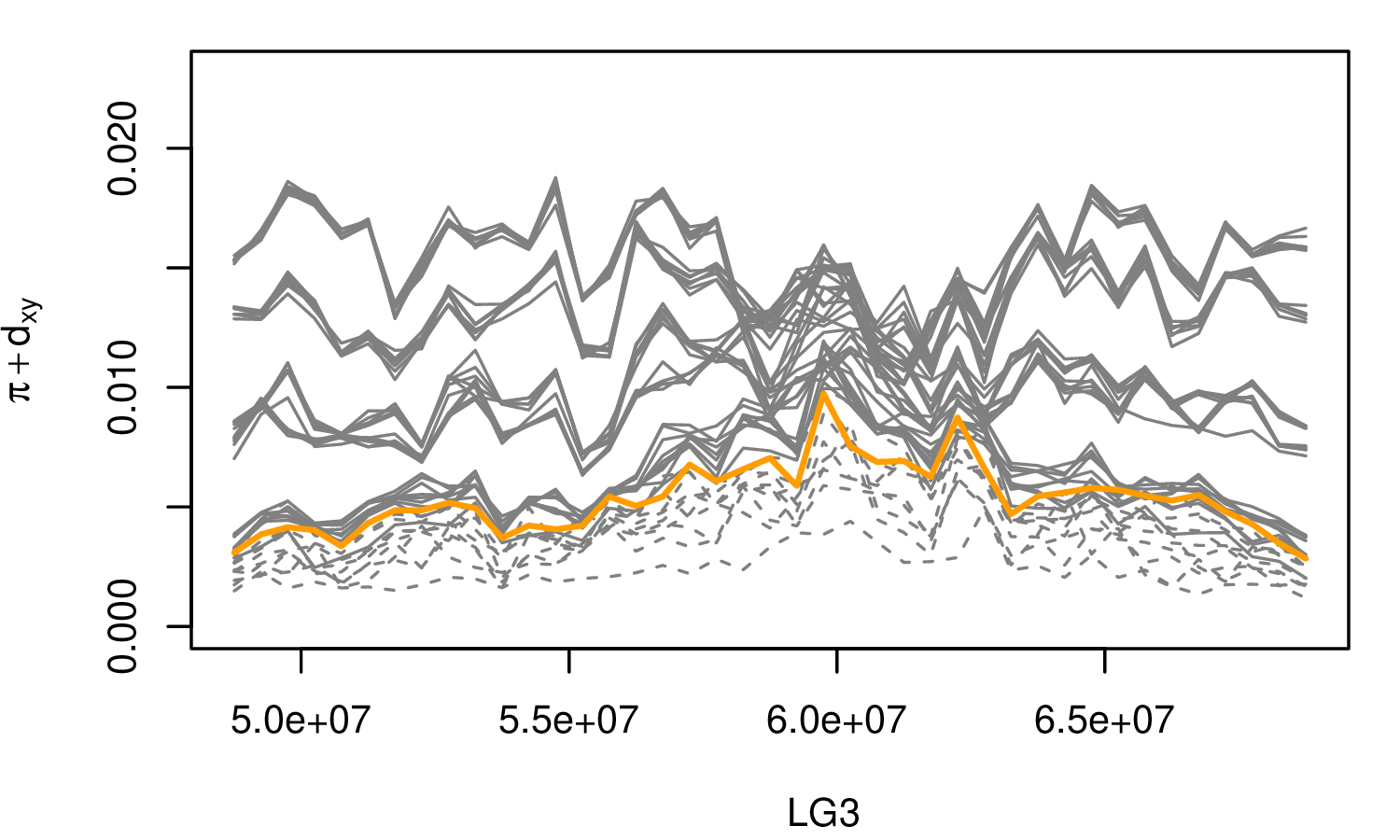
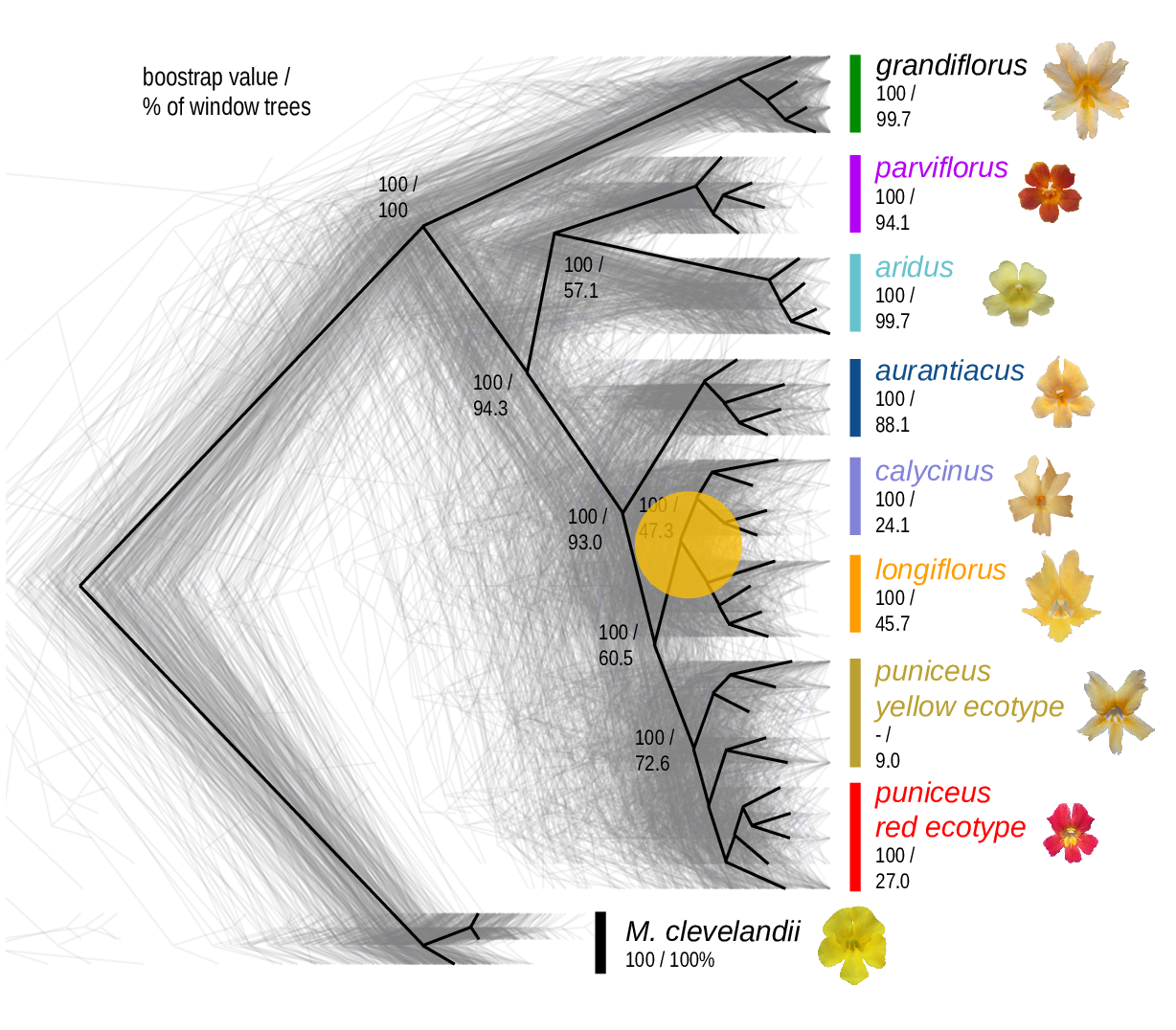
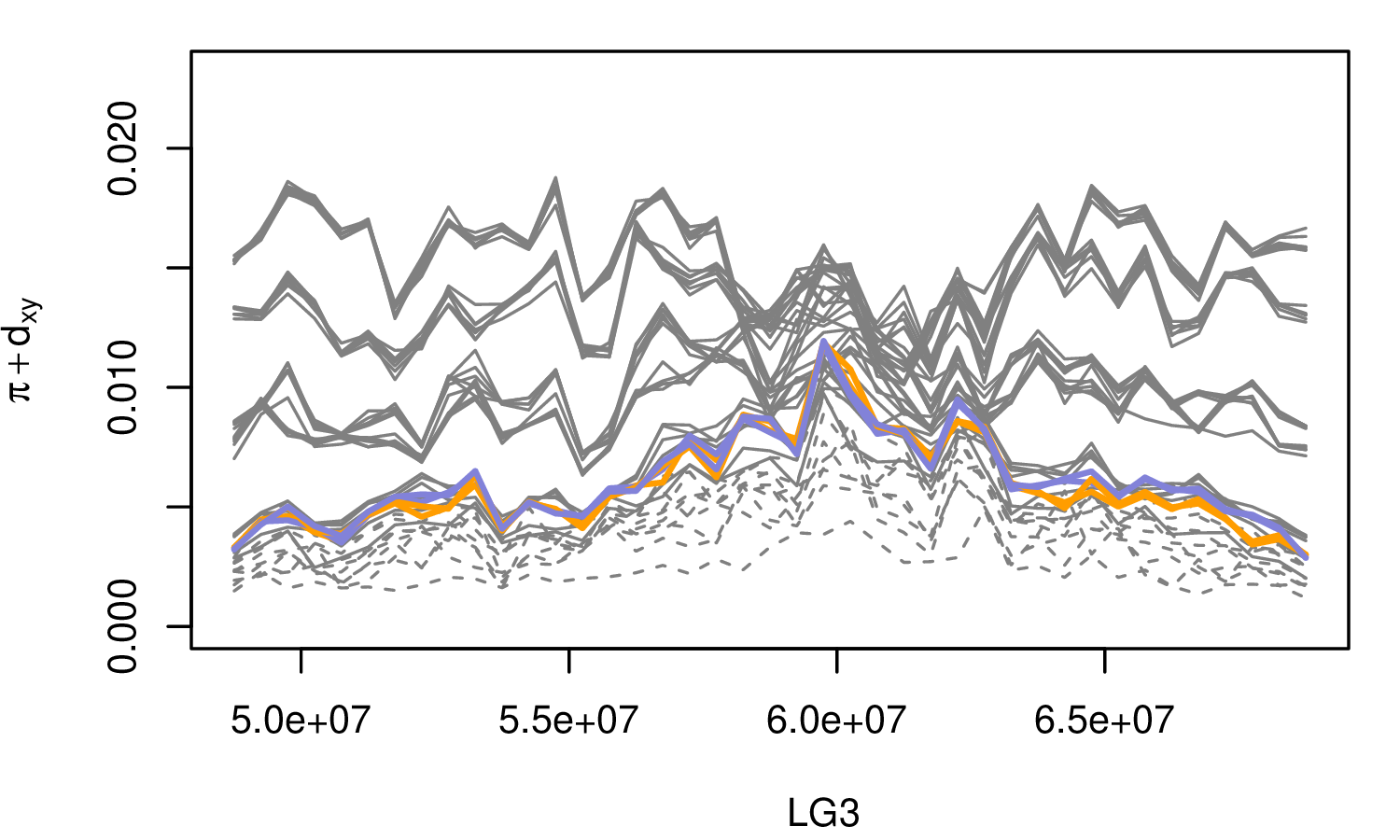
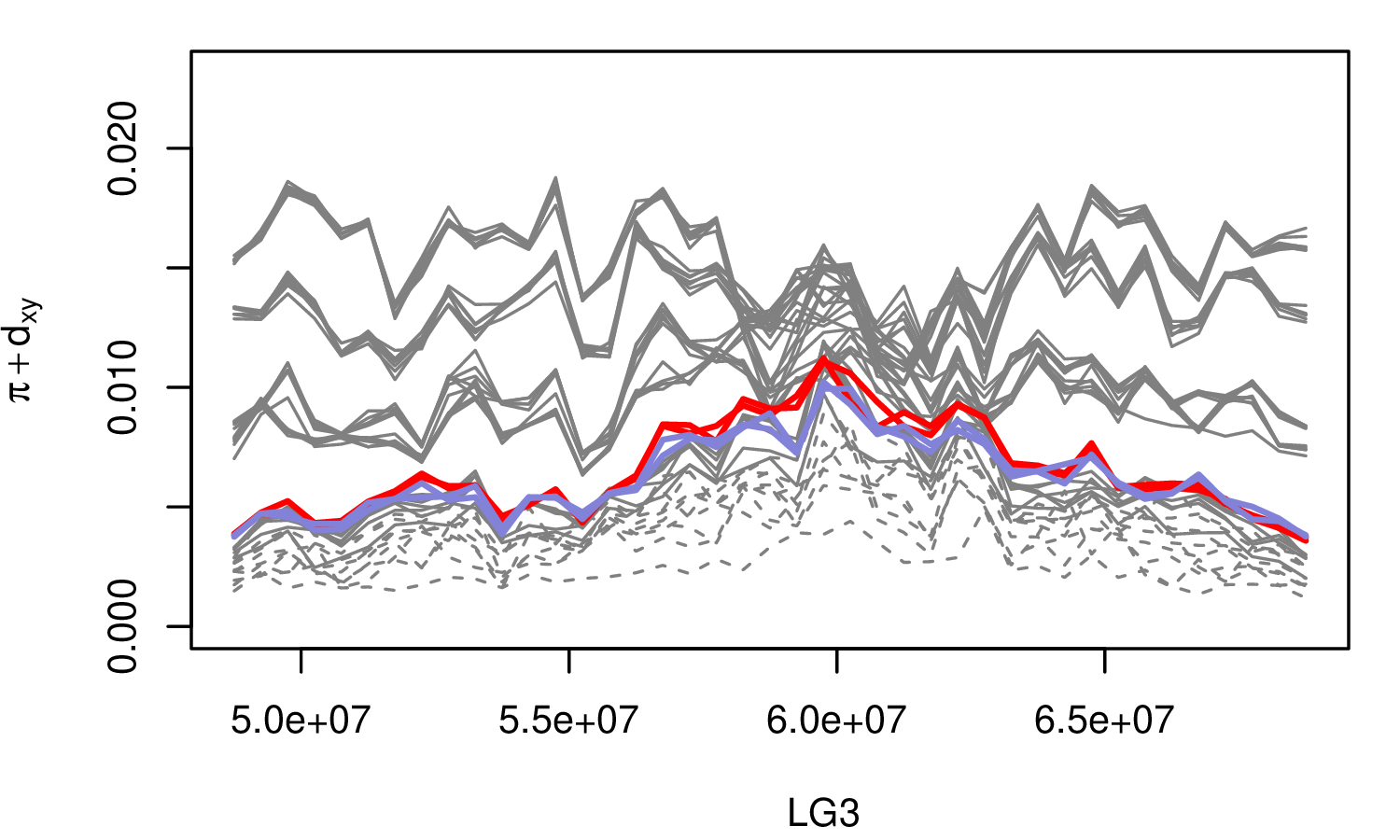
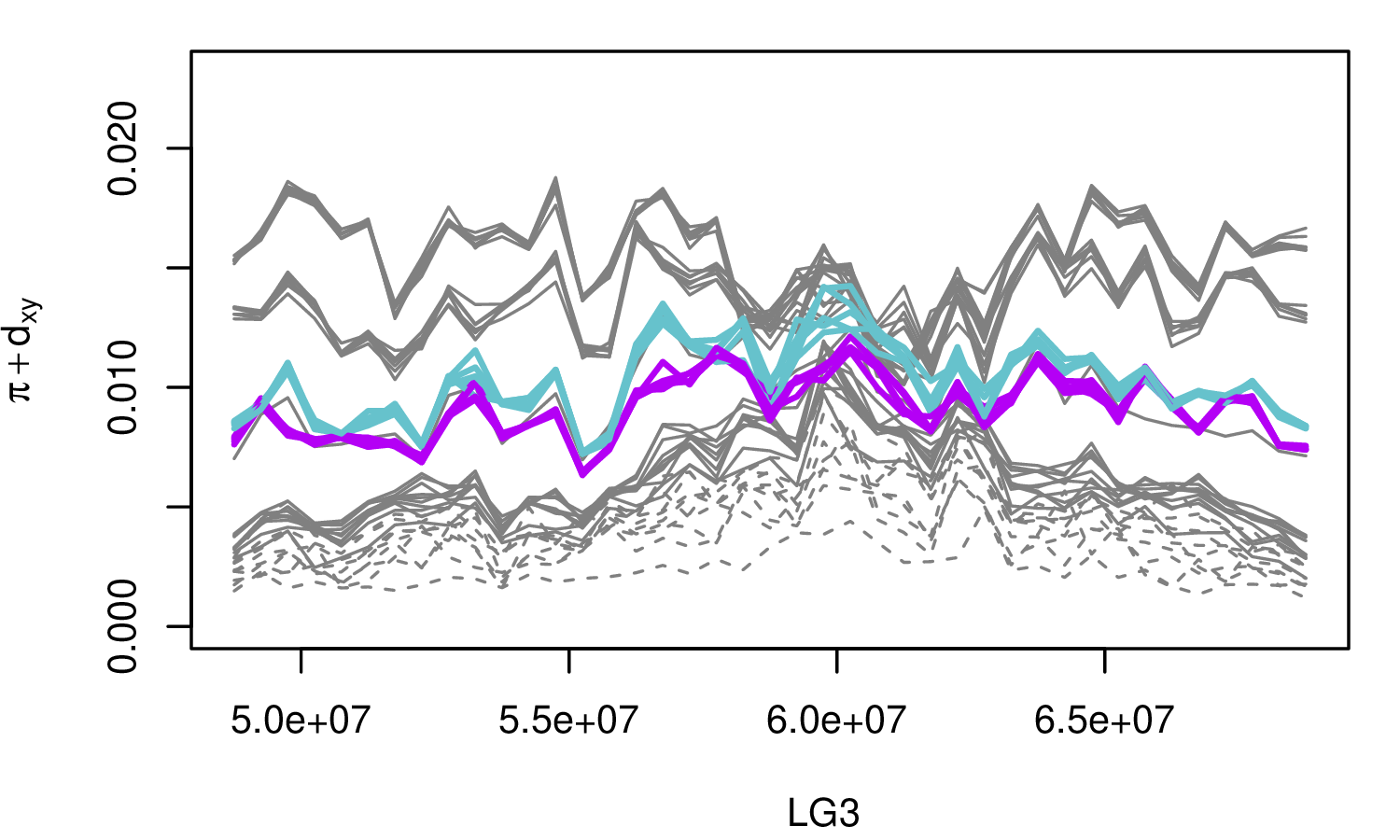
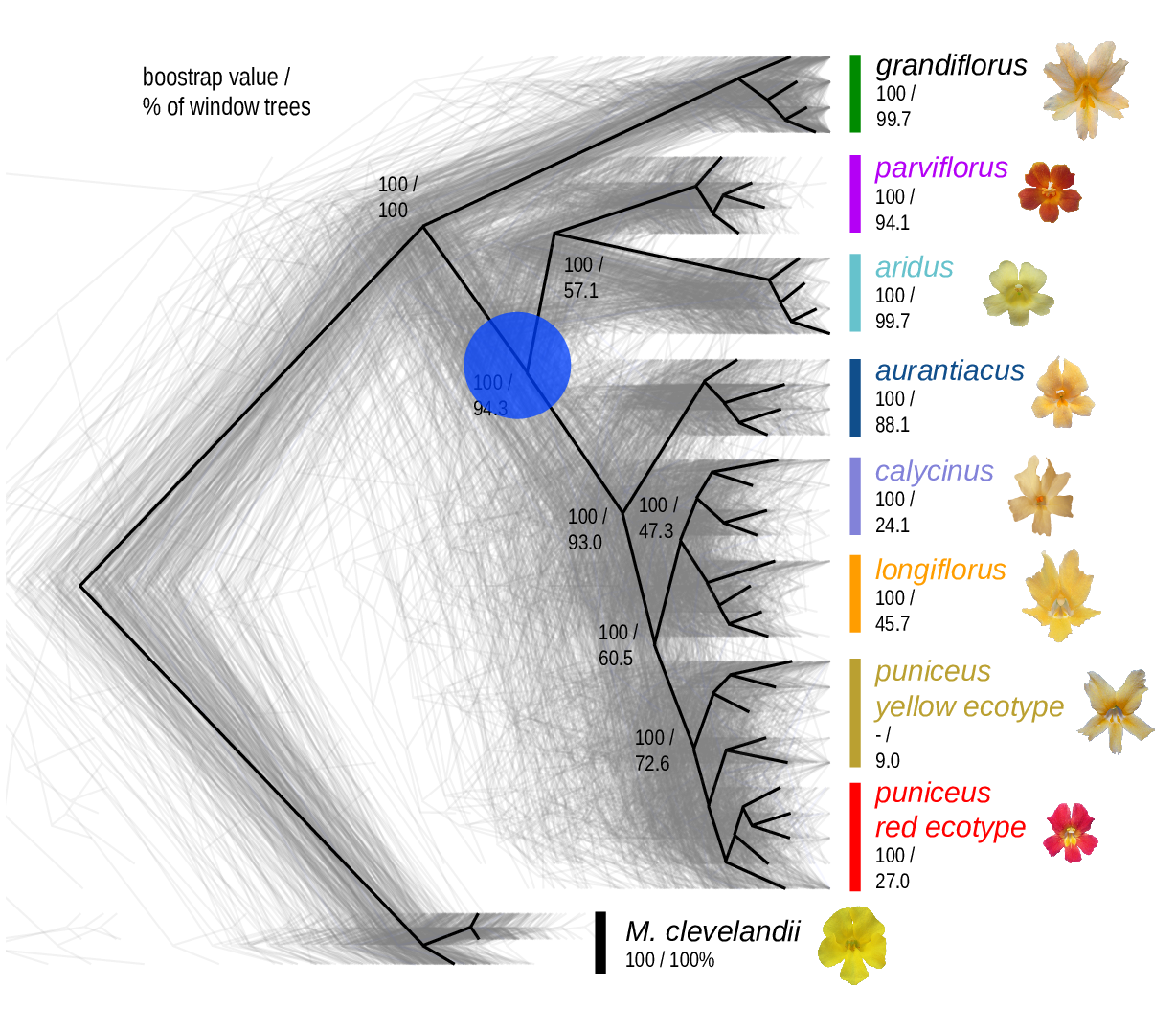
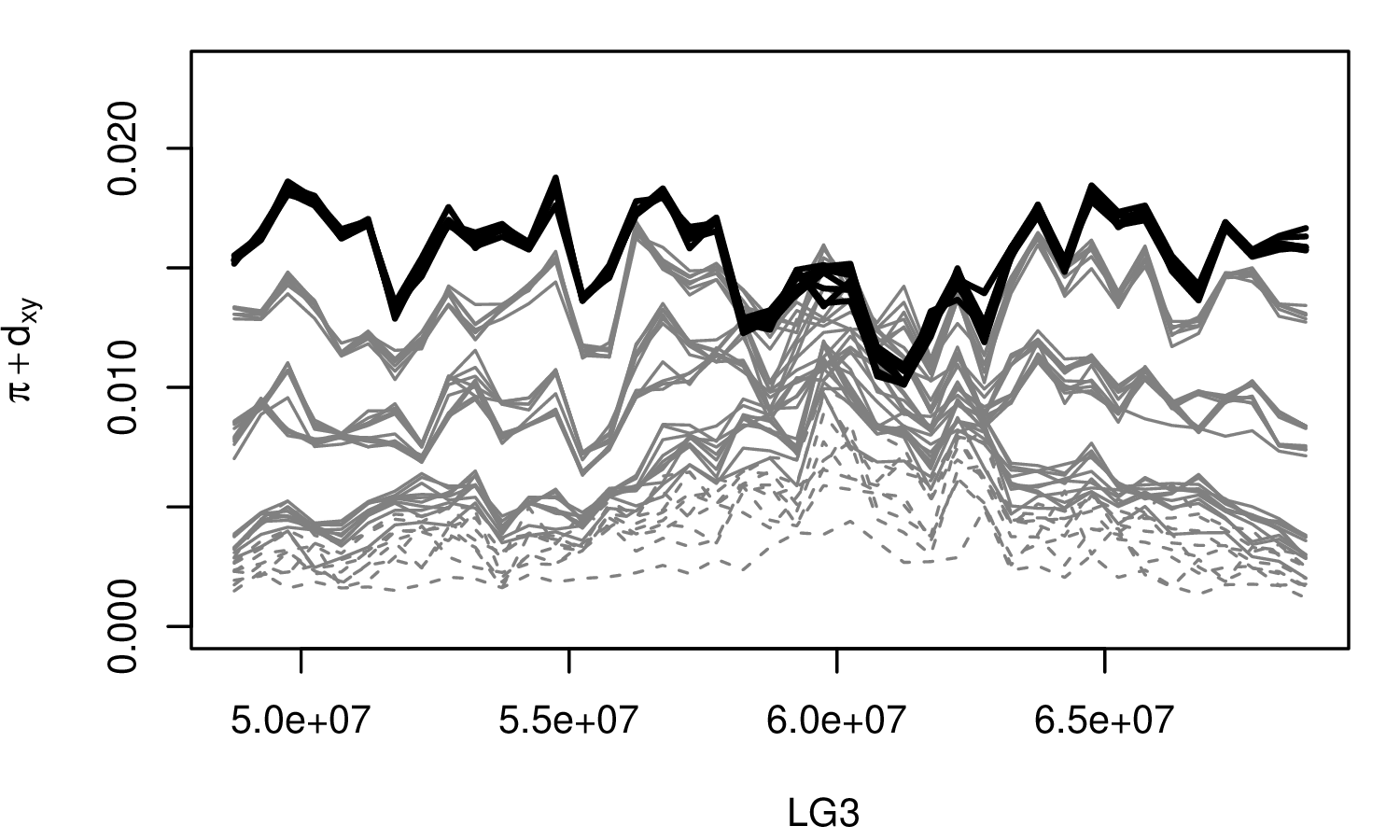
\[ \begin{aligned} \pi &= \text{ (within-pop genetic distance) } \\ d_{xy} &= \text{ (between-pop genetic distance) } \end{aligned} \]

Some questions

How much genetic variation typically underlies traits?

How important is natural selection in determining genetic diversity?

How will populations respond to changes in the future?

To test theories and fit models, we need simulations with realistic

  1. population sizes,
  2. genomes,
  3. selective pressures,
  4. histories, and
  5. geography.

The tree sequence

History is a sequence of trees

For a set of sampled chromosomes, at each position along the genome there is a genealogical tree that says how they are related.

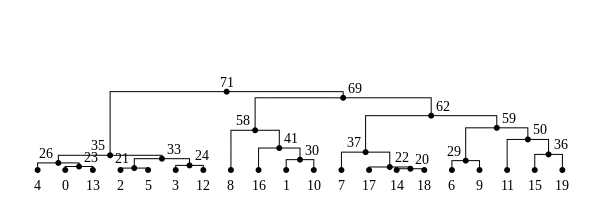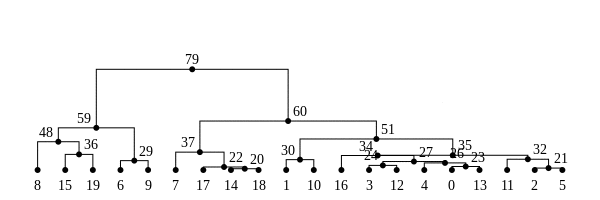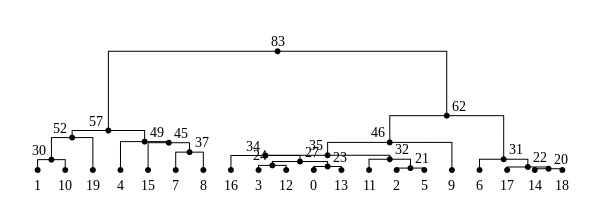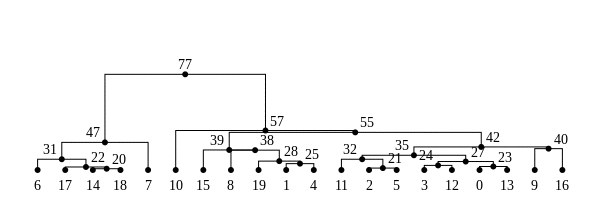
Trees along a chromosome
Trees along a chromosome

The tree sequence is a way to describe this, er, sequence of trees.

genotypes
genotypes
genotypes and a tree
genotypes and a tree
genotypes and the next tree
genotypes and the next tree

Kelleher, Etheridge, and McVean introduced the tree sequence data structure for a fast coalescent simulator, msprime.

  • stores sequence and genealogical data very efficiently

  • tree-based sequence storage closely related to haplotype-matching compression

  • python/C tskit tools

jerome kelleher
jerome kelleher

jerome kelleher

File sizes

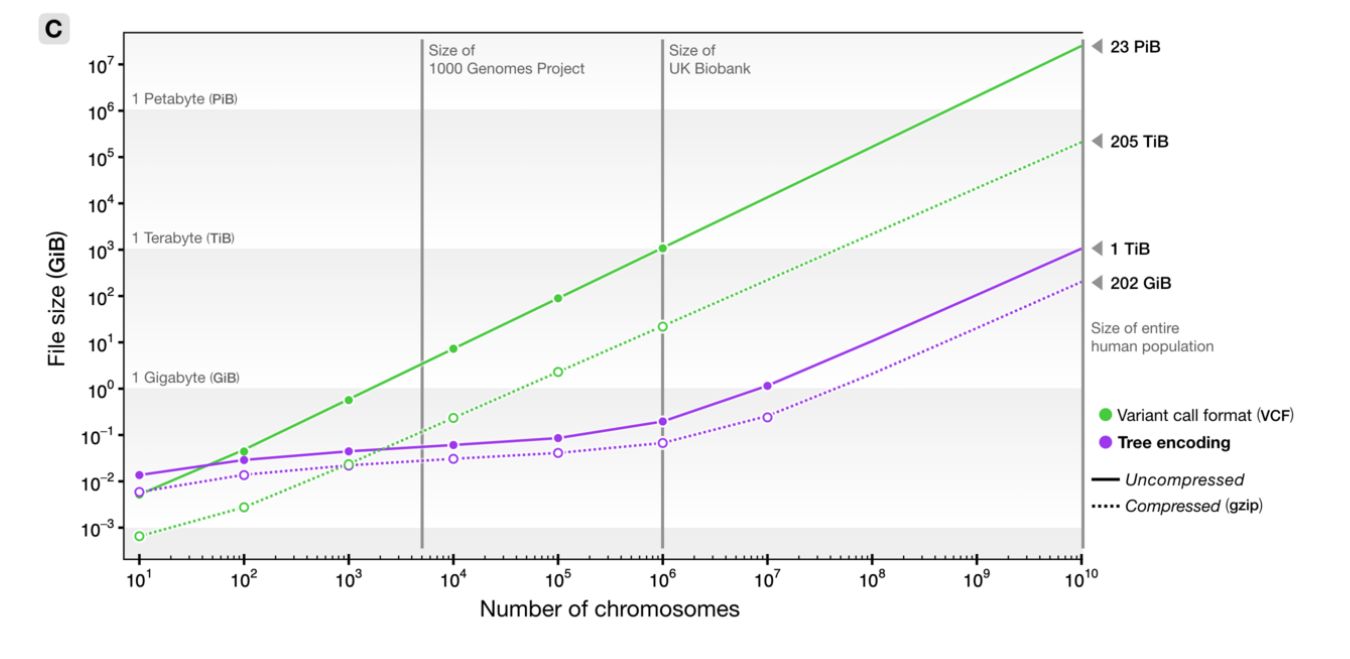
file sizes
file sizes

from Kelleher et al 2018, Inferring whole-genome histories in large population datasets, Nature Genetics

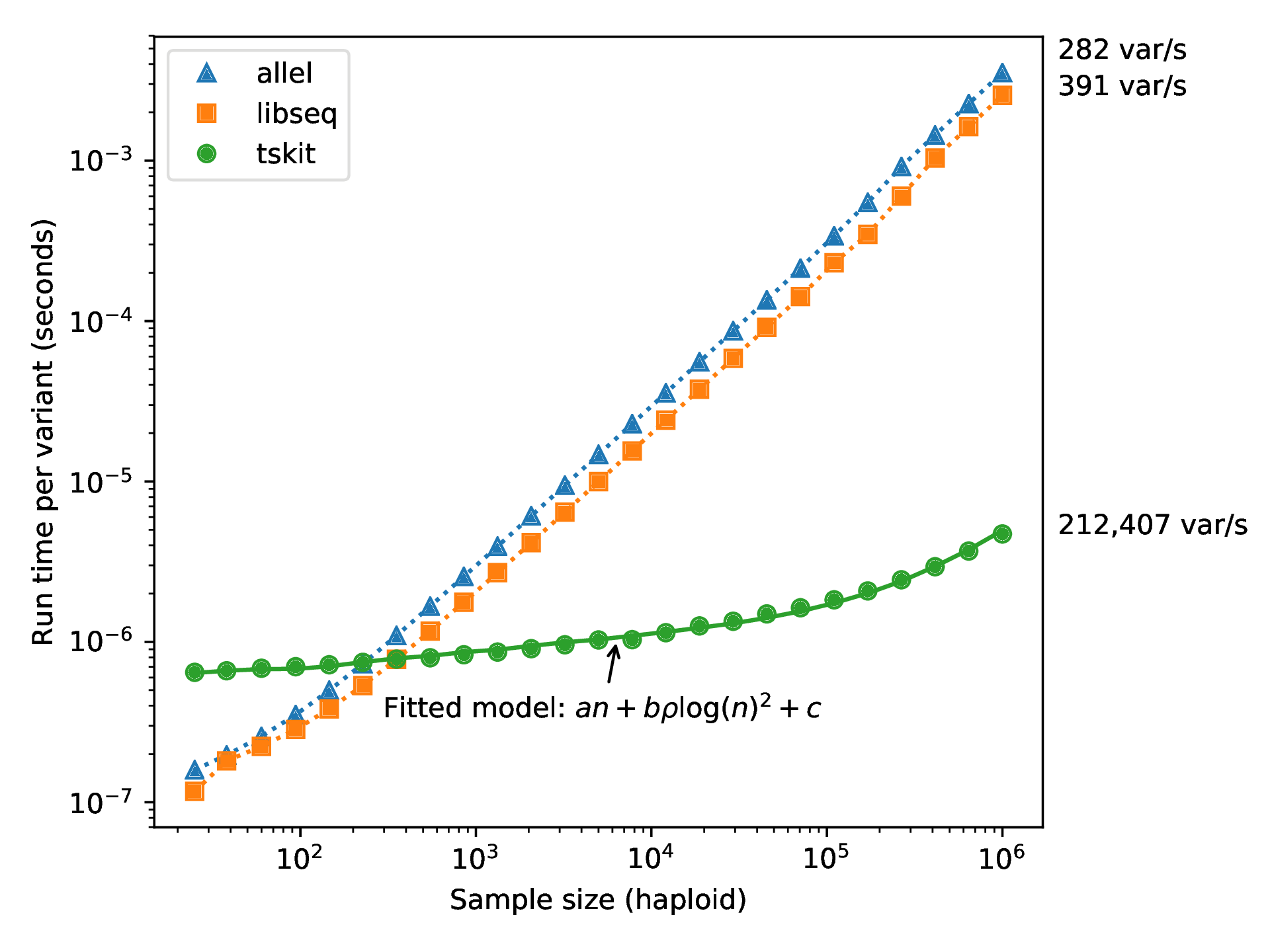
Computation run time

efficiency of treestat computation
efficiency of treestat computation

from Ralph, Thornton and Kelleher 2019, Efficiently summarizing relationships in large samples, bioRxiv

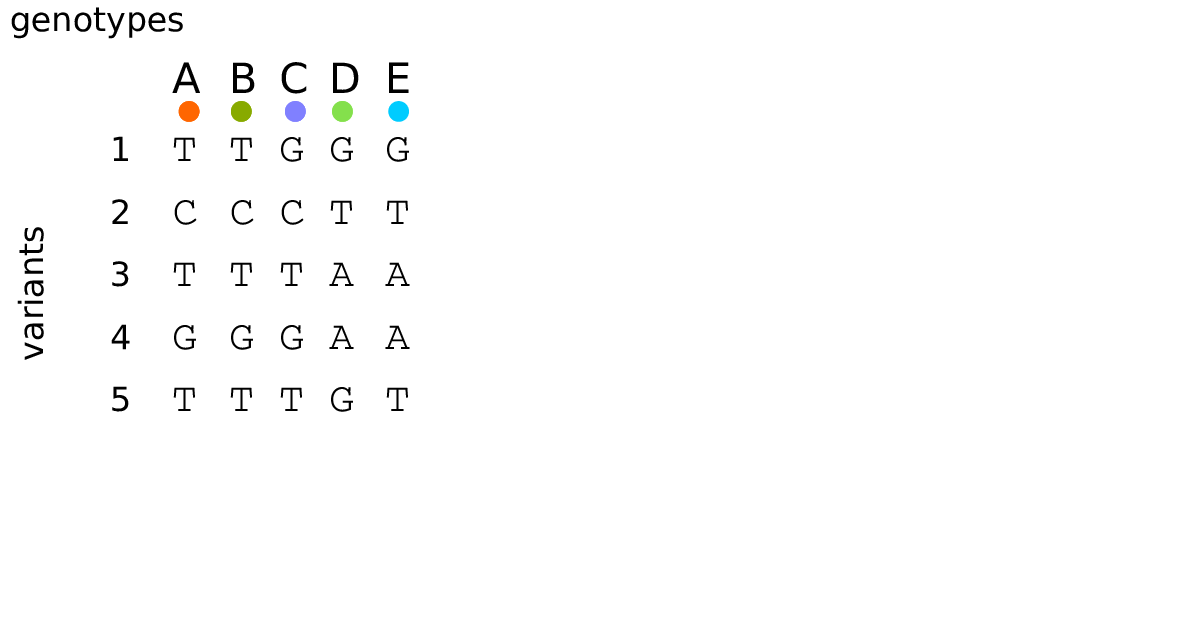
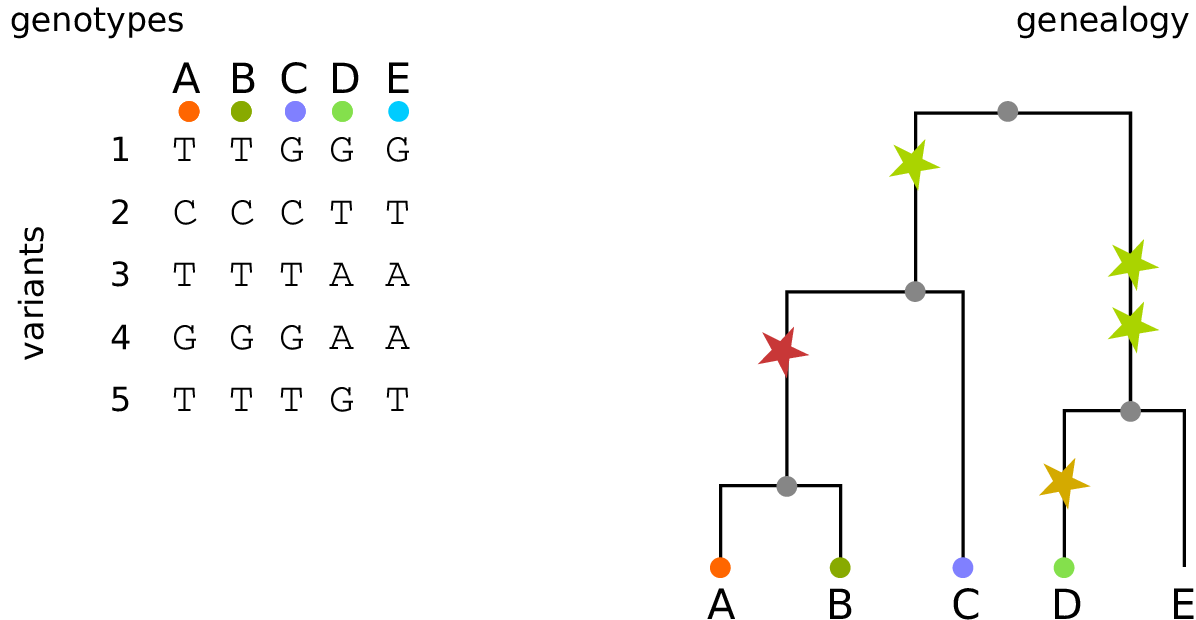
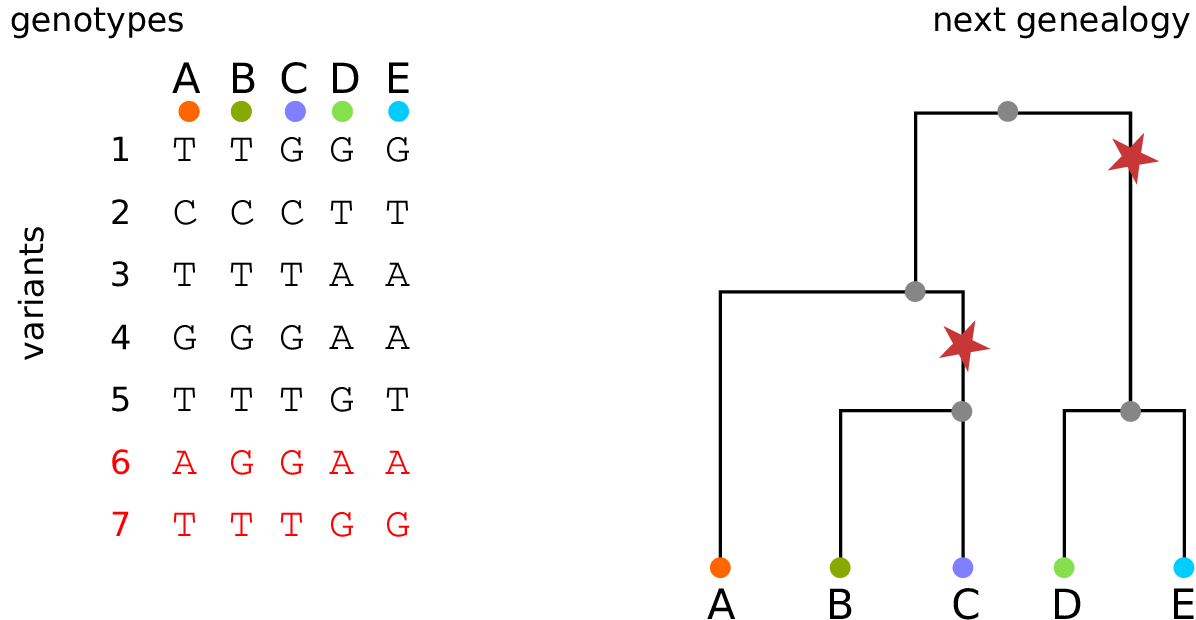
What do genotypes tell us about the genealogies?

also from Ralph, Thornton and Kelleher 2019, Efficiently summarizing relationships in large samples, bioRxiv

Summaries of genotypes and genealogies

Genotypes:

  1. For each site,
  2. look at who has which alleles,
  3. and add a summary of these values to our running total.

Example: genetic distance counts how many mutations differ between two sequences.

Summaries of genotypes and genealogies

Genotypes:

  1. For each site,
  2. look at who has inherited which alleles,
  3. and add a summary of these values to the running total.

Example: sequence divergence counts how many mutations differ between two sequences.

Trees:

  1. For each branch,
  2. look at who would inherit mutations on that branch,
  3. and add the expected contribution to the running total.

Example: the mean time to most recent common ancestor between two sequences.

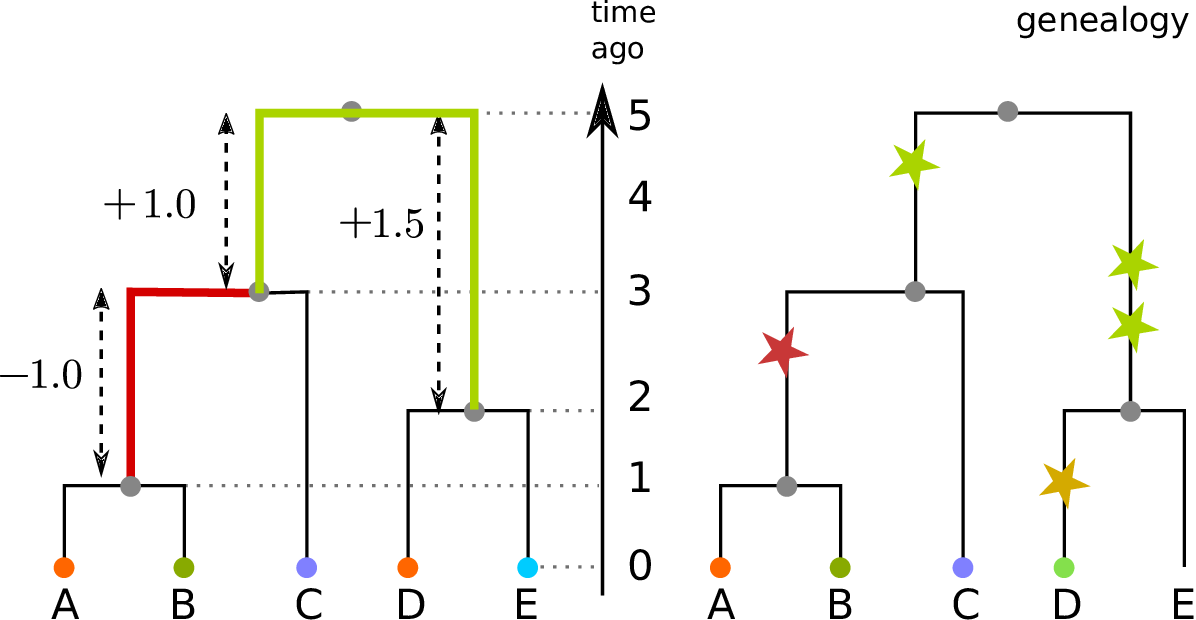
site and branch stats
site and branch stats

Duality

Any set of sample weights \(w\) and summary function \(f\) defines both

  • a statistic of genotypes, \(\text{Site}(f,w)\), and
  • a statistic of genealogies, \(\text{Branch}(f,w)\).

With genealogies fixed, and averaging only over mutations with rate \(\mu\), \[\begin{equation} \text{Branch}(f, w) = \frac{1}{\mu} \E\left[ \text{Site}(f, w) \right] . \end{equation}\]

Dealing directly with genealogies can remove the layer of noise due to mutation: \[\begin{equation} \frac{1}{\mu^2} \var\left[\text{Site}(f,w)\right] = \var\left[\text{Branch}(f,w)\right] + \frac{1}{n} \E\left[\text{Branch}(f^2,w)\right] \end{equation}\]

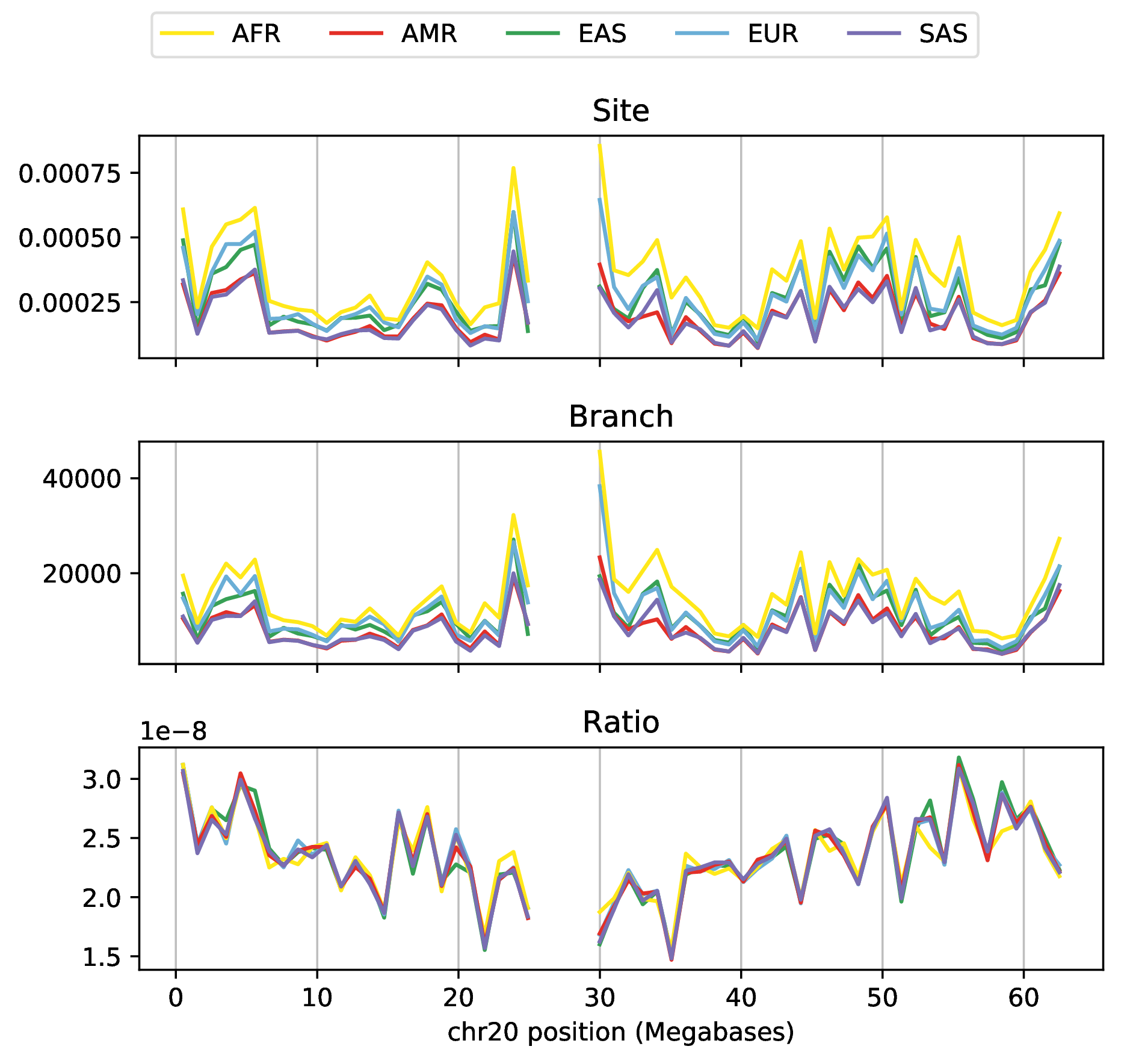
duality in 1000G data
duality in 1000G data

Duality, on 1000 Genomes data? Not quite…

  • variation in mutation rate?
  • biased gene conversion?
  • selection?
  • inference artifacts?

Tree sequence from Speidel et al 2019.

Application to demographic inference

Erik Lundgren: “Isolation By Coalescence”

  • fits a discrete random walk model to lineage movement
  • genetic distance \(\approx\) mean coalescence time

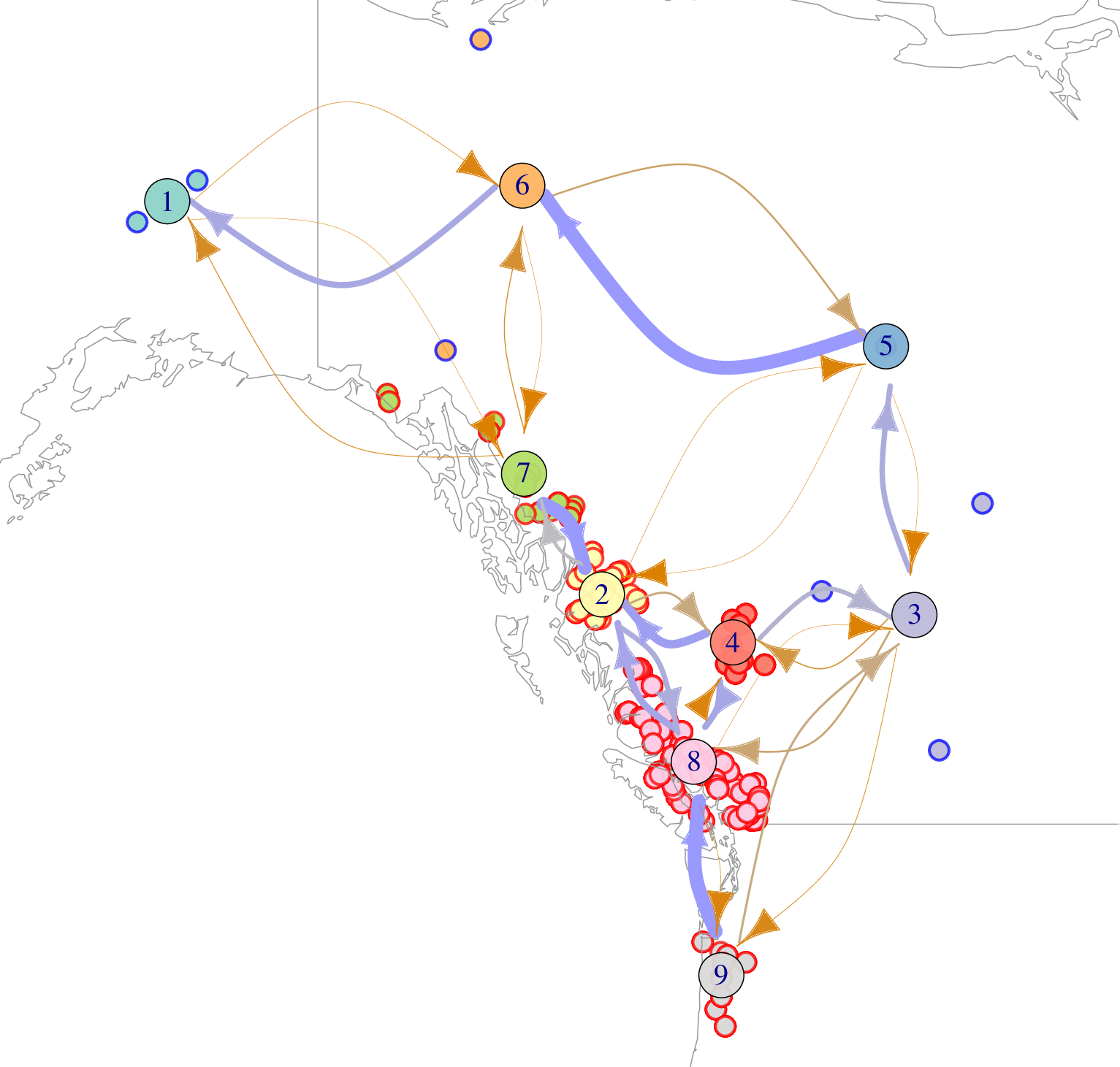
From Lundgren and Ralph, 2019, Are populations like a circuit?

Populus trichocarpa and P. balsamifera data from Moreno Geraldes et al 2014

  • glacial refugia
  • postglacial expansion

Application to genomic simulations

The main idea

If we record the tree sequence that relates everyone to everyone else,

after the simulation is over we can put neutral mutations down on the trees.

Since neutral mutations don’t affect demography,

this is equivalent to having kept track of them throughout.

From Kelleher, Thornton, Ashander, and Ralph 2018, Efficient pedigree recording for fast population genetics simulation.

and Haller, Galloway, Kelleher, Messer, and Ralph 2018, Tree‐sequence recording in SLiM opens new horizons for forward‐time simulation of whole genomes

jared galloway jaime ashander

This means recording the entire genetic history of everyone in the population, ever.

It is not clear this is a good idea.

But, with a few tricks…

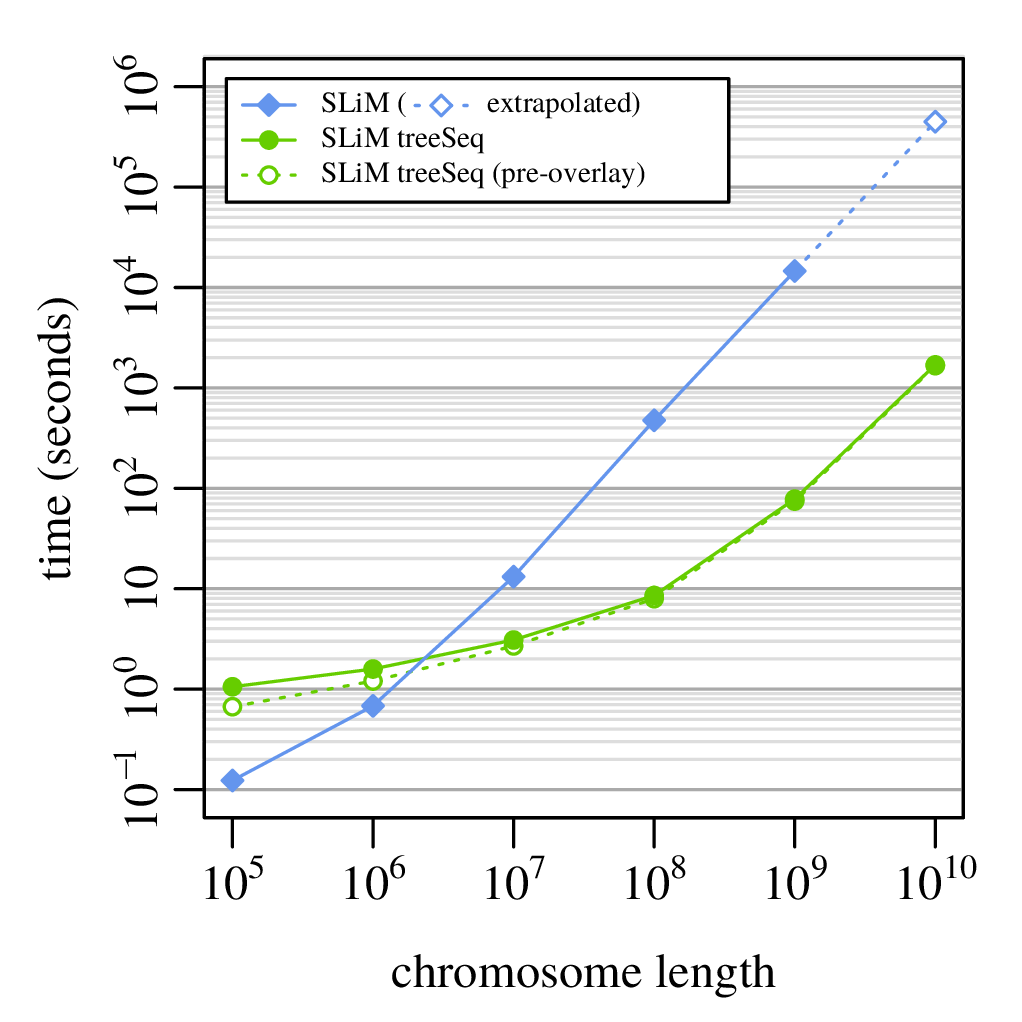
A 100x speedup!

What else can you do with tree sequences?

  • record ancient samples
  • true ancestry reconstruction
  • recapitation: fast, post-hoc initialization with coalescent simulation

For example:

  • genome as human chr7 (\(1.54 \times 10^8\)bp)
  • \(\approx\) 10,000 diploids
  • 500,000 overlapping generations
  • continuous, square habitat
  • selected mutations at rate \(10^{-10}\)
  • neutral mutations added afterwards

Runtime: 8 hours

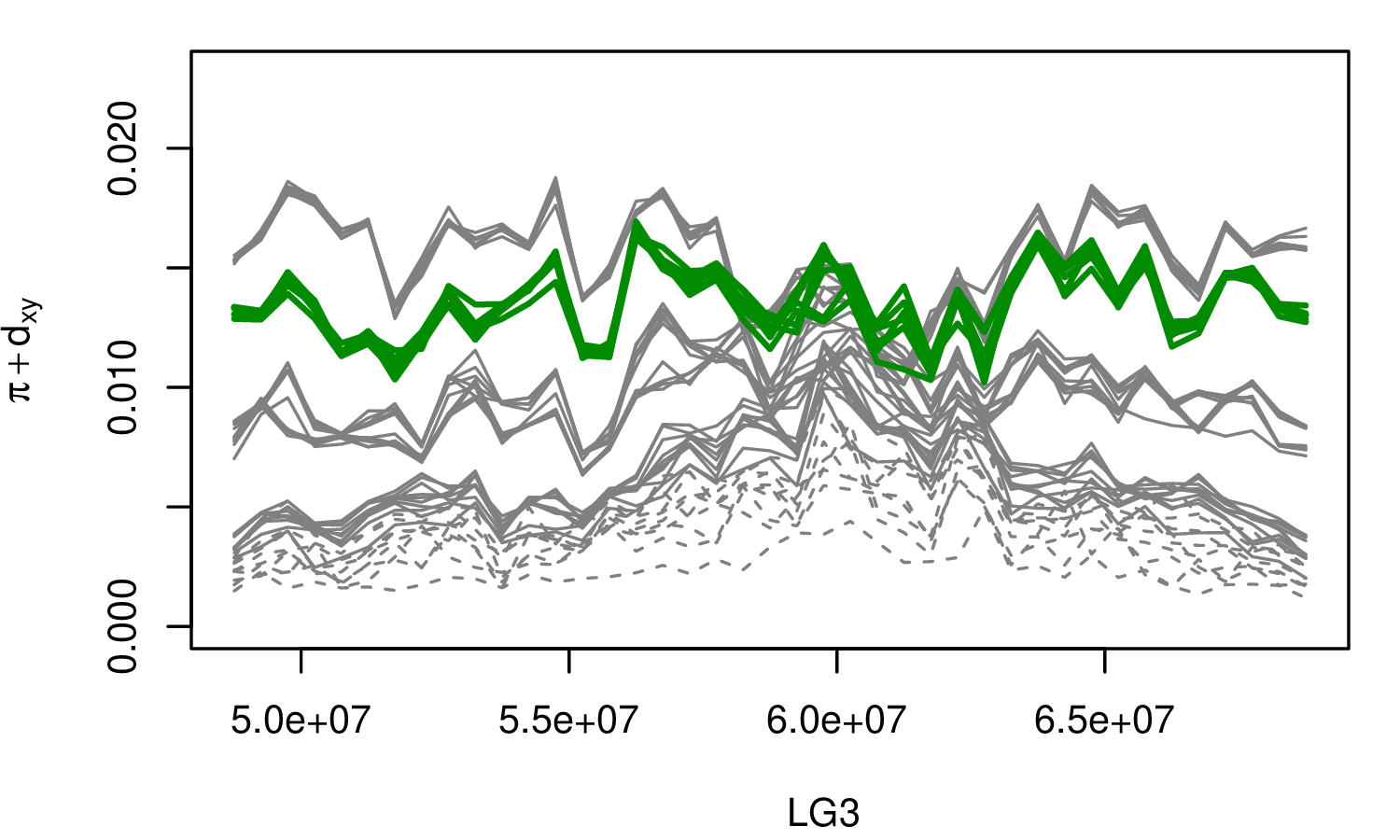
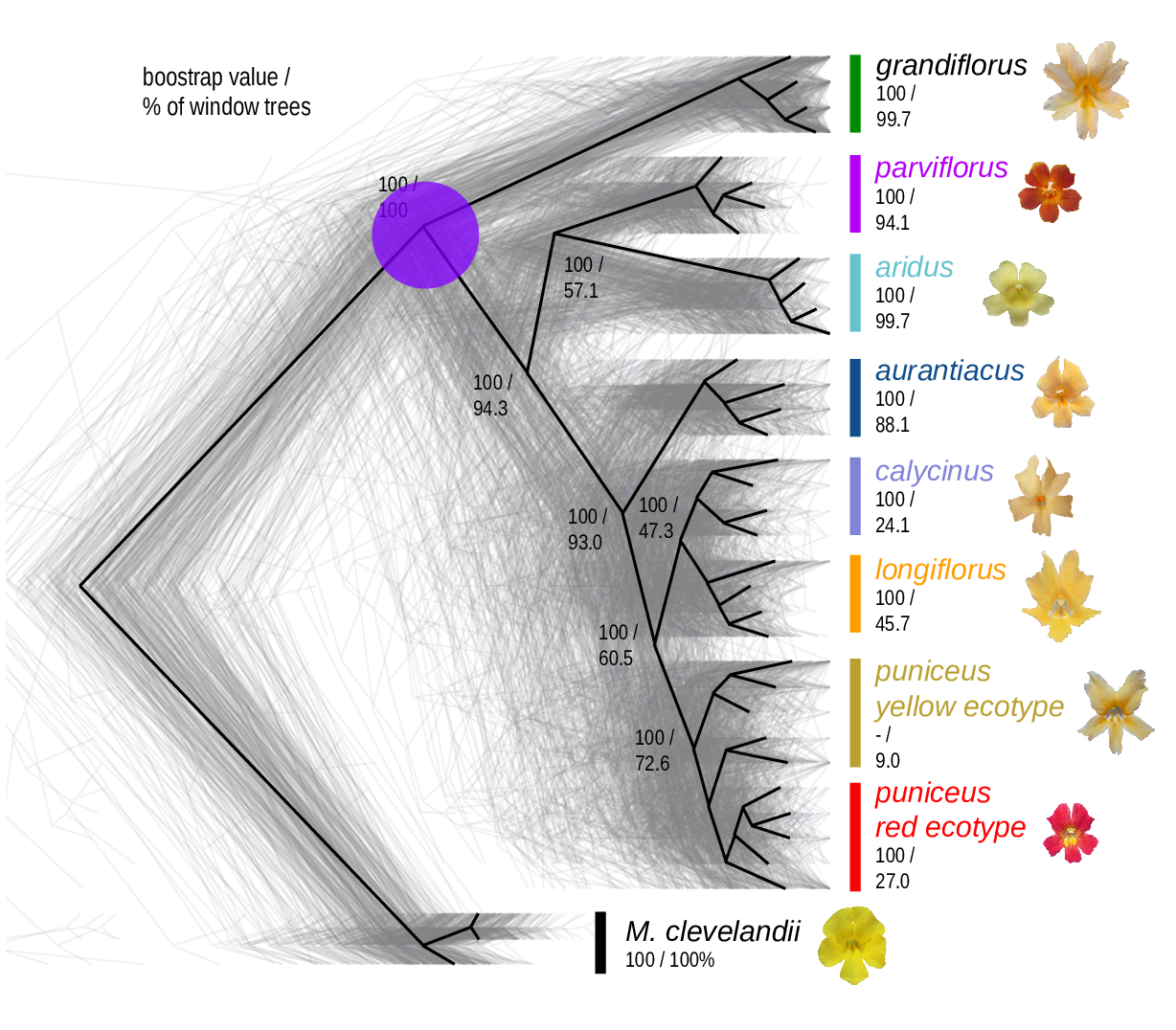
Back to Mimulus

The data

Simulations

  • \(N=10,000\) diploids
  • burn-in for \(10N\) generations

  • population split, with either:

    • neutral
    • background selection
    • selection against introgressed alleles

Murillo Rodrigues

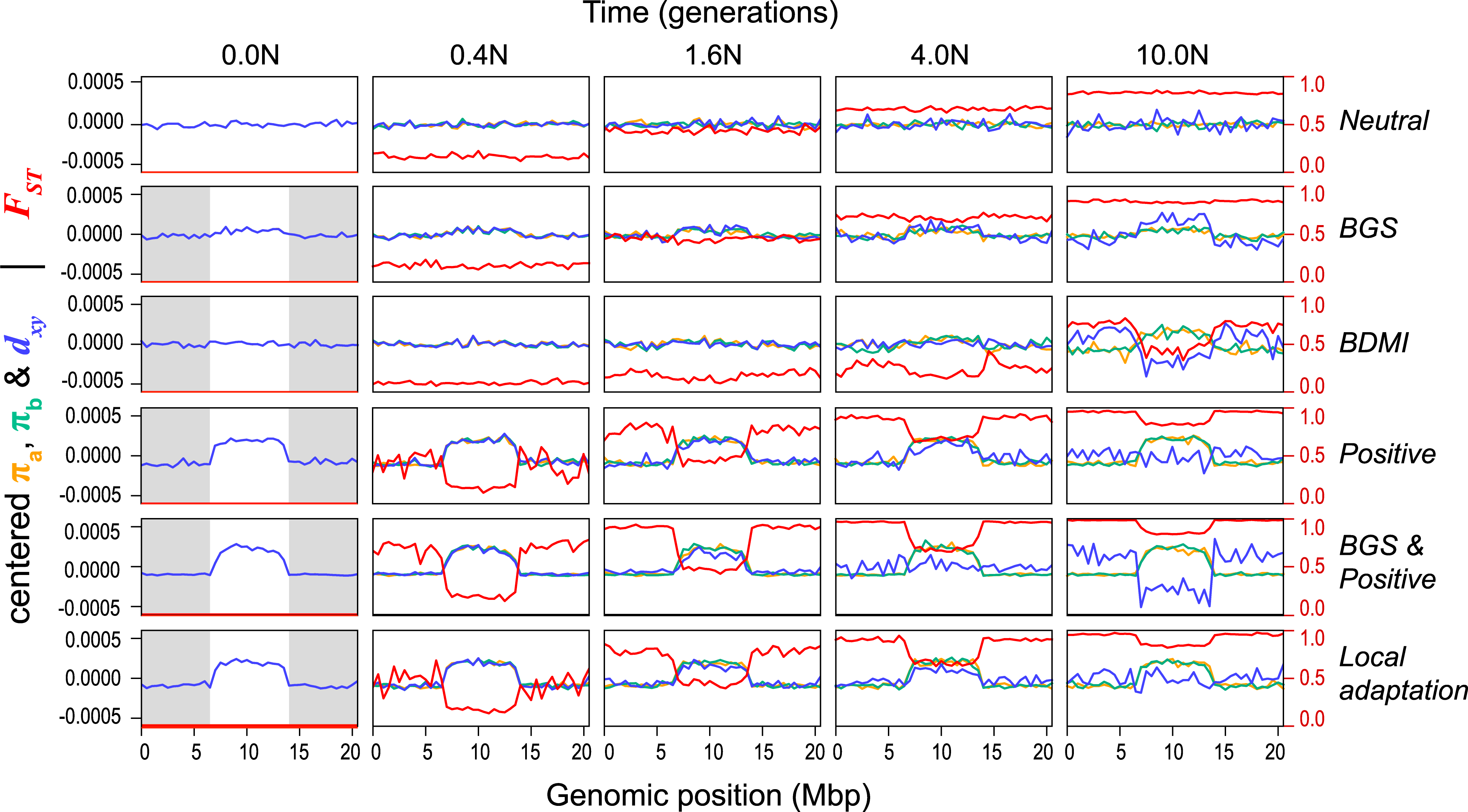
From Widespread selection and gene flow shape the genomic landscape during a radiation of monkeyflowers, Sean Stankowski, Madeline A. Chase, Allison M. Fuiten, Murillo F. Rodrigues, Peter L. Ralph, and Matthew A. Streisfeld; PLoS Bio 2019.

Wrap-up

We need better understanding and prediction of how

  1. genotype maps to phenotype,
  2. natural selection acts on phenotypes,
  3. and that affects genetic variation.

To test theories and fit models, we need simulations with realistic

  1. population sizes,
  2. genomes,
  3. selective pressures,
  4. histories, and
  5. geography.

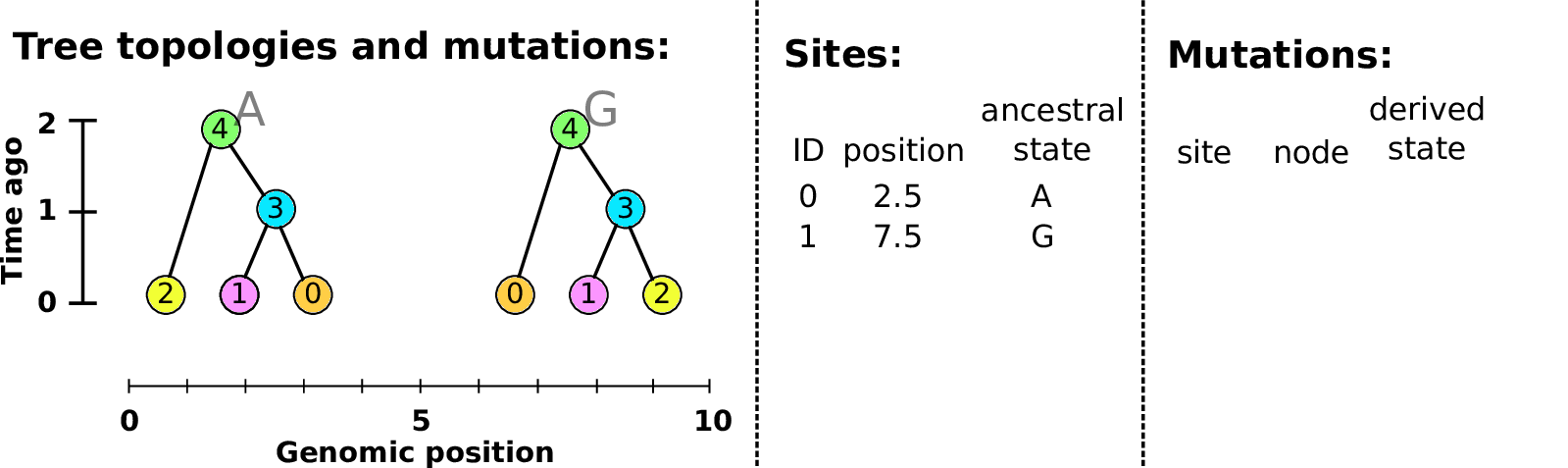
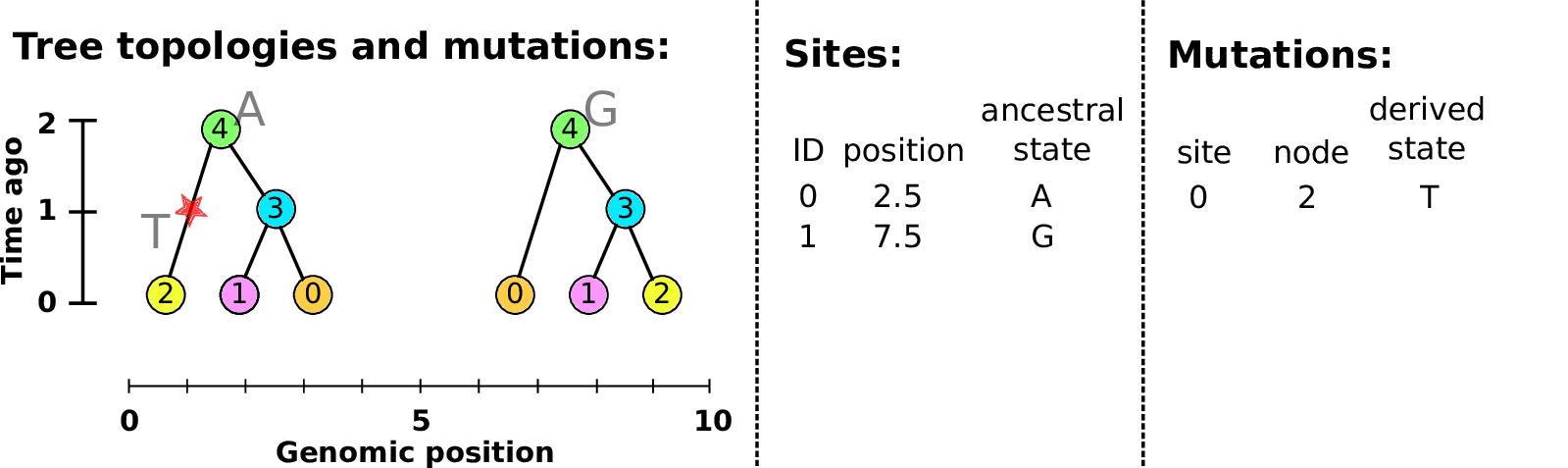
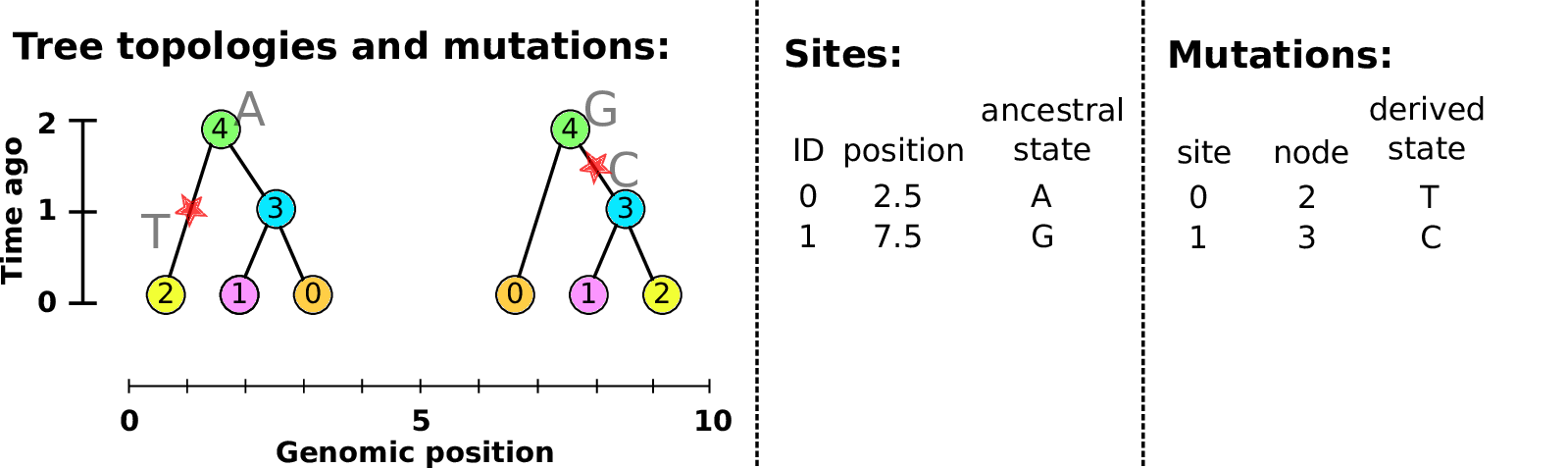
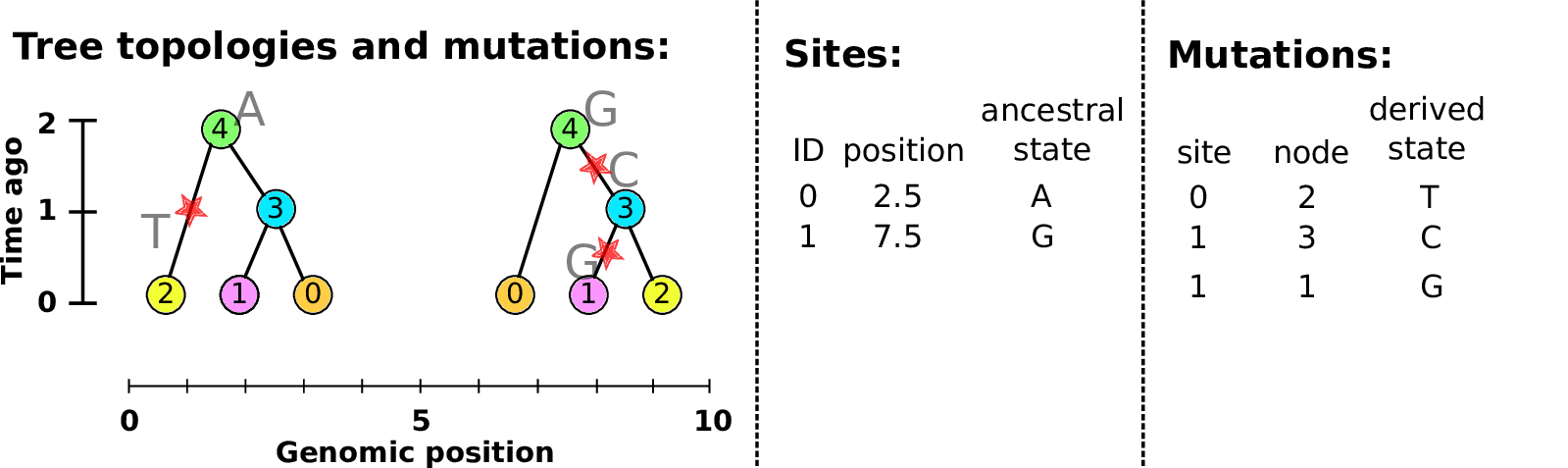
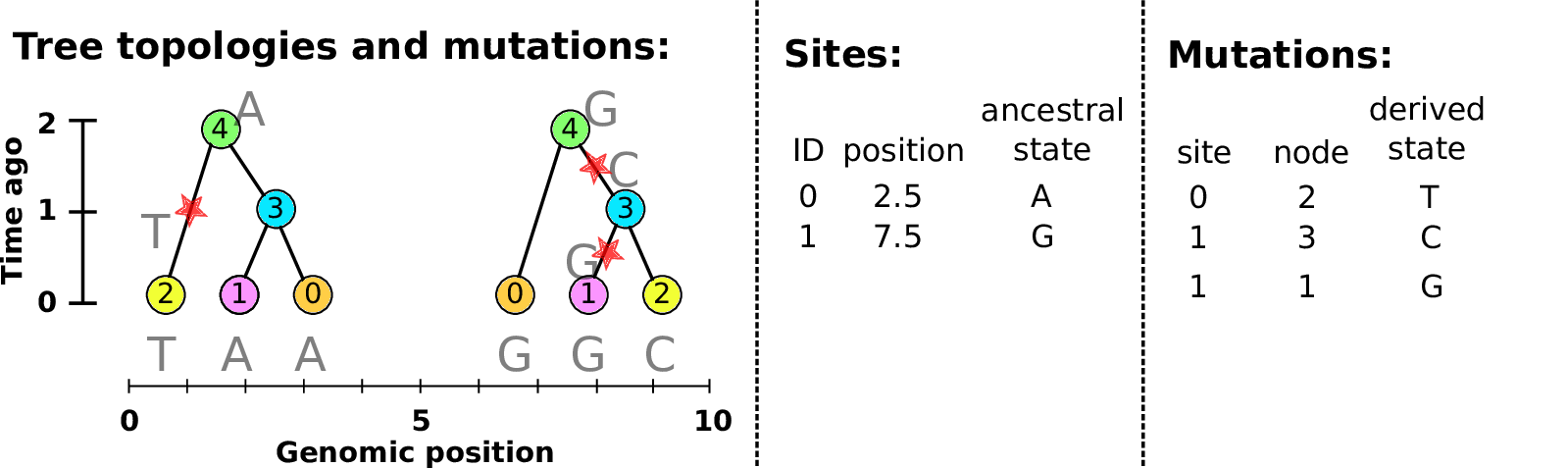
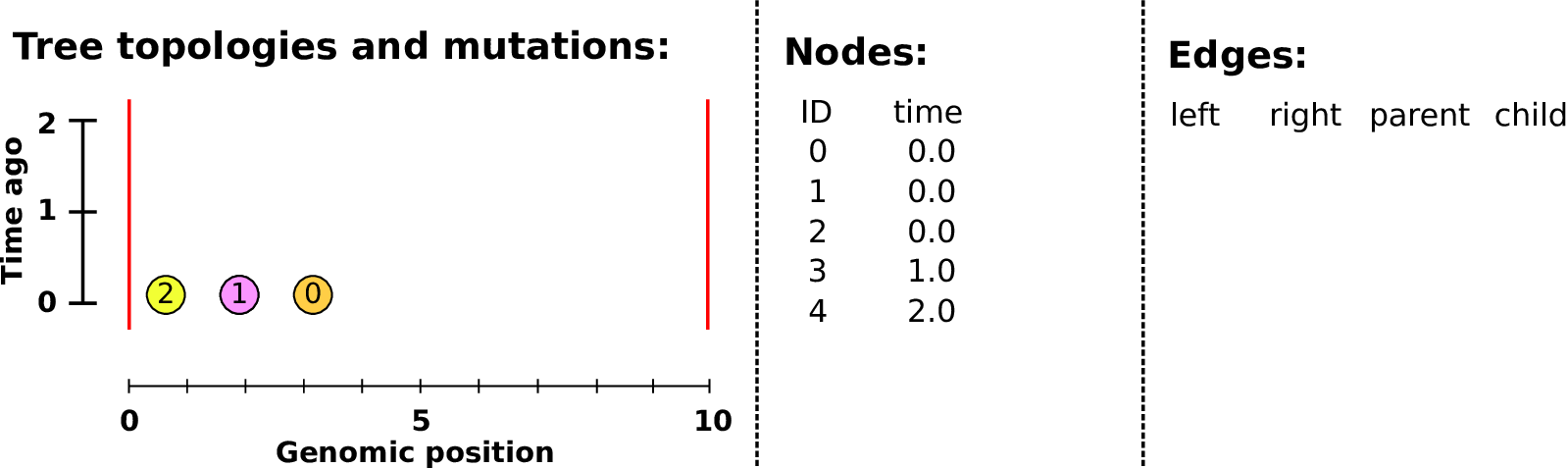
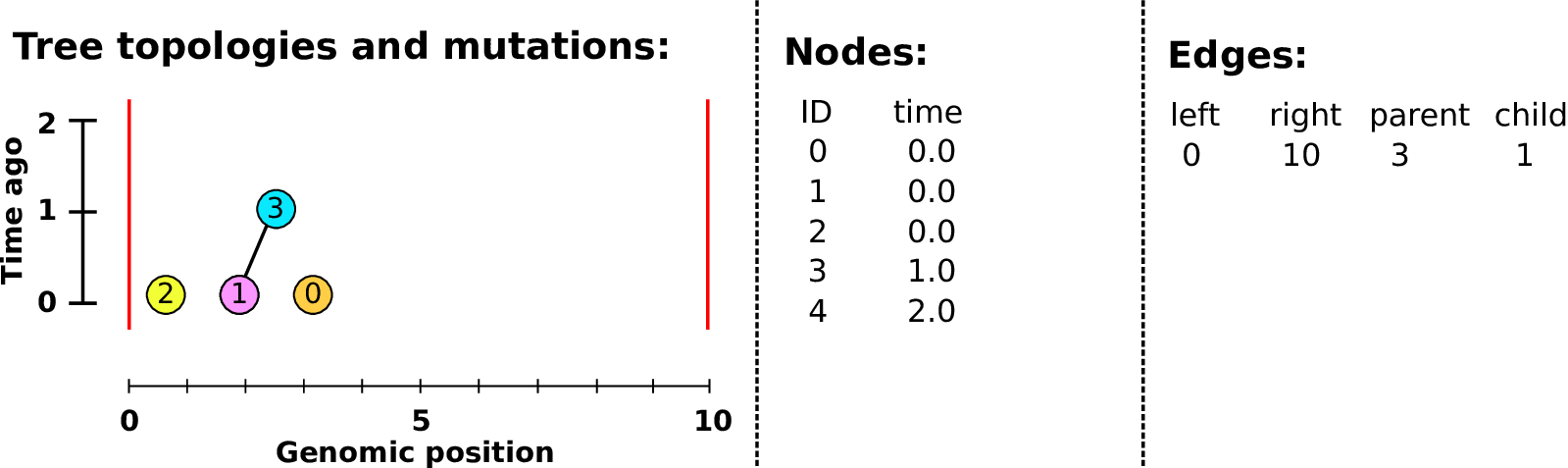
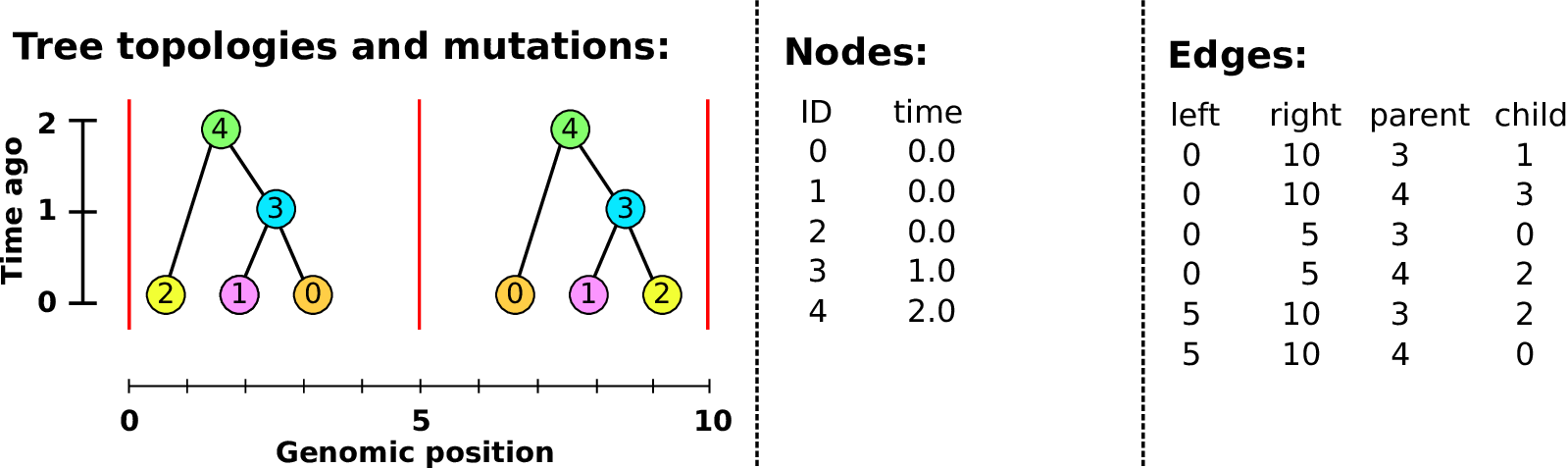
An example tree sequence

Example: three samples; two trees; two variant sites

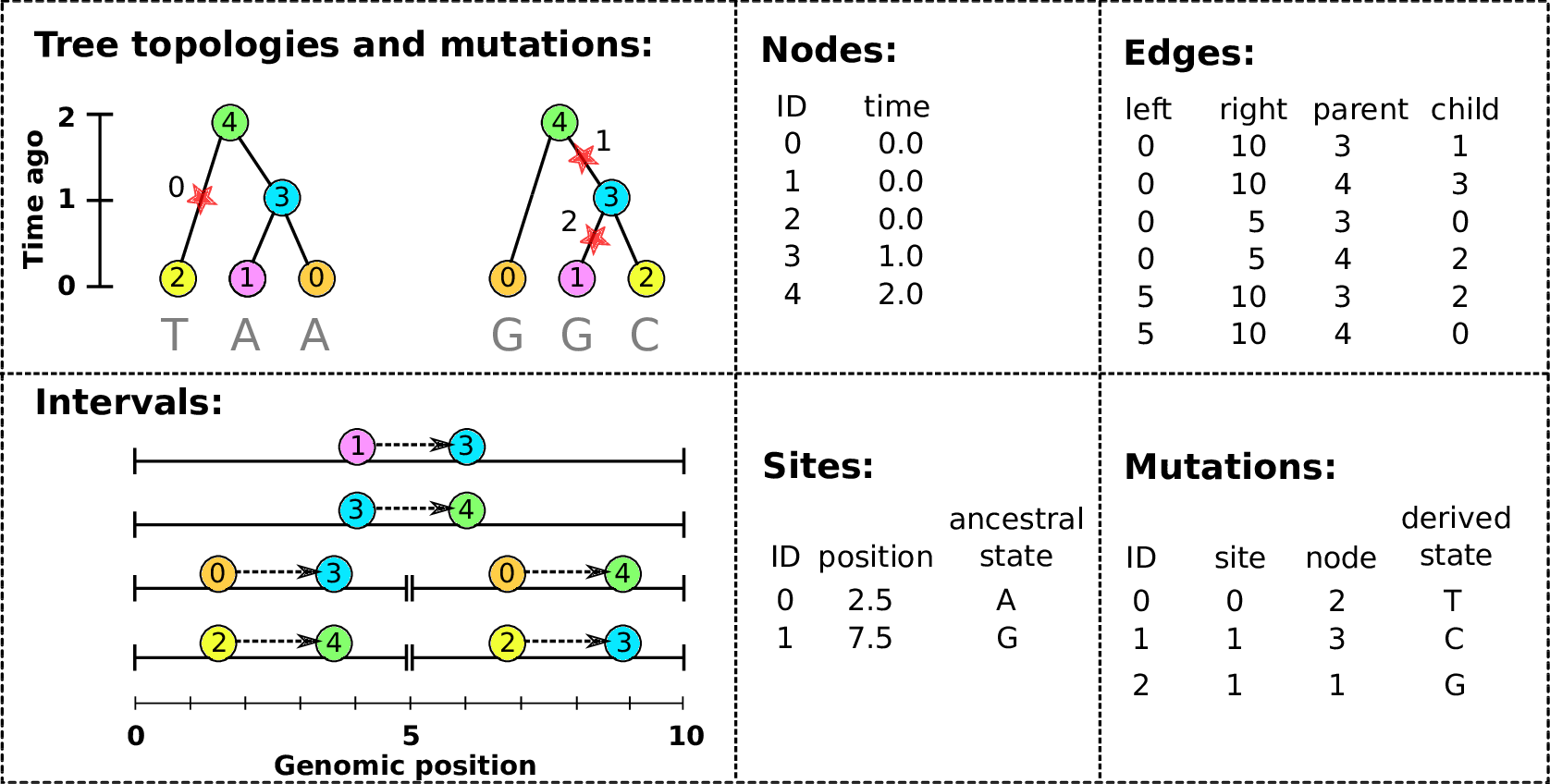
Example tree sequence
Example tree sequence

Nodes and edges

Edges

Who inherits from who; only necessary for coalescent events.

Records: interval (left, right); parent node; child node.

Nodes

The ancestors those happen in.

Records: time ago (of birth); ID (implicit).

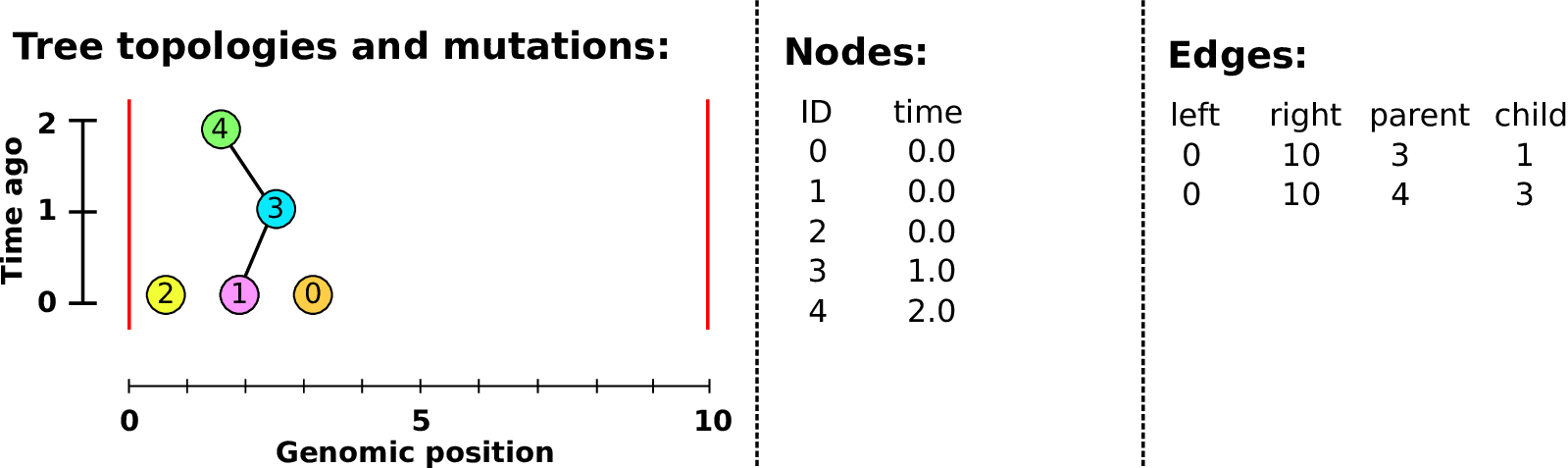
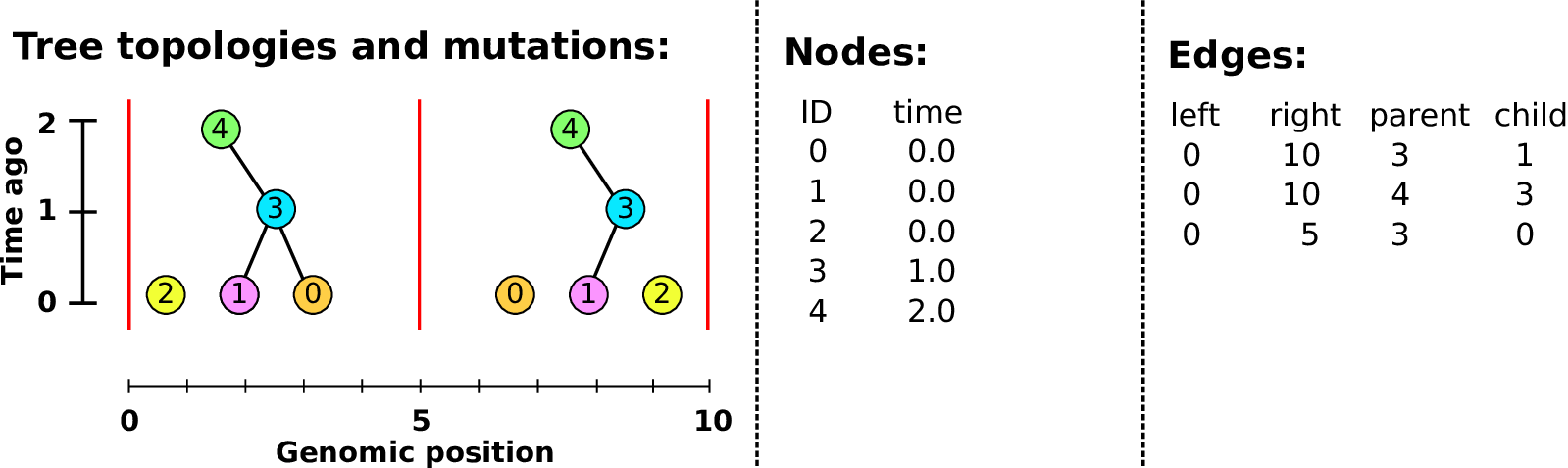
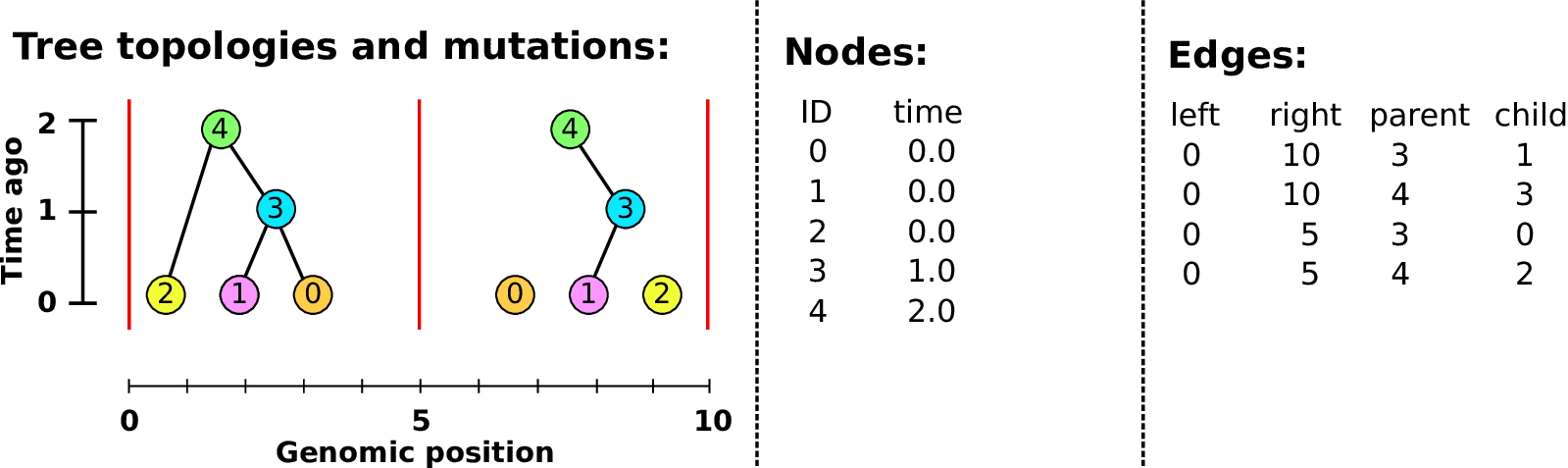
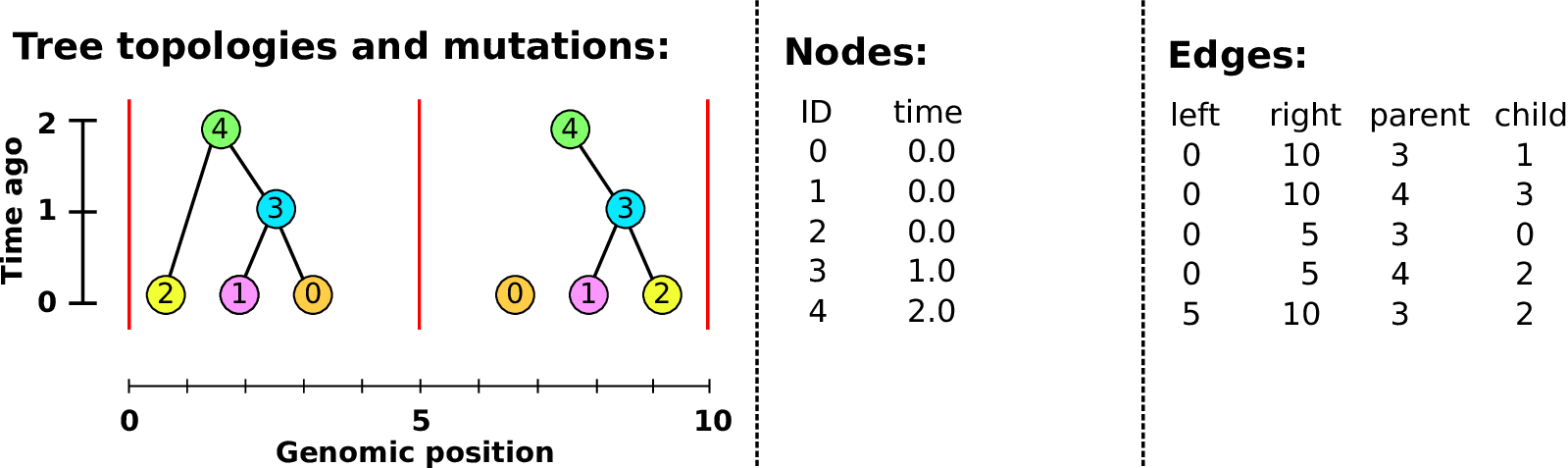
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence
Building a tree sequence

Sites and mutations

Mutations

When state changes along the tree.

Records: site it occured at; node it occurred in; derived state.

Sites

Where mutations fall on the genome.

Records: genomic position; ancestral (root) state; ID (implicit).

Adding mutations
Adding mutations
Adding mutations
Adding mutations
Adding mutations
Adding mutations
Adding mutations
Adding mutations
Adding mutations
Adding mutations