Pushing the boundaries of population genomic computation with the tree sequence
Peter Ralph
Center for Genome Research and Biocomputing
Oregon State // 26 May 2021
Outline
Outline of the talk
- What do we need simulations for?
- The tree sequence
- Applications
Simulation-based inference
Some questions
What forces contribute to the variation in genetic diversity along the genome? (explaining variation in diversity)
Which locations along the genome have been the recent targets of positive natural selection? (identifying sweeps)
Where did this individual come from? (inferring location)
How do organisms disperse across the landscape? (dispersal maps)
Inverse problems

Inverse problems
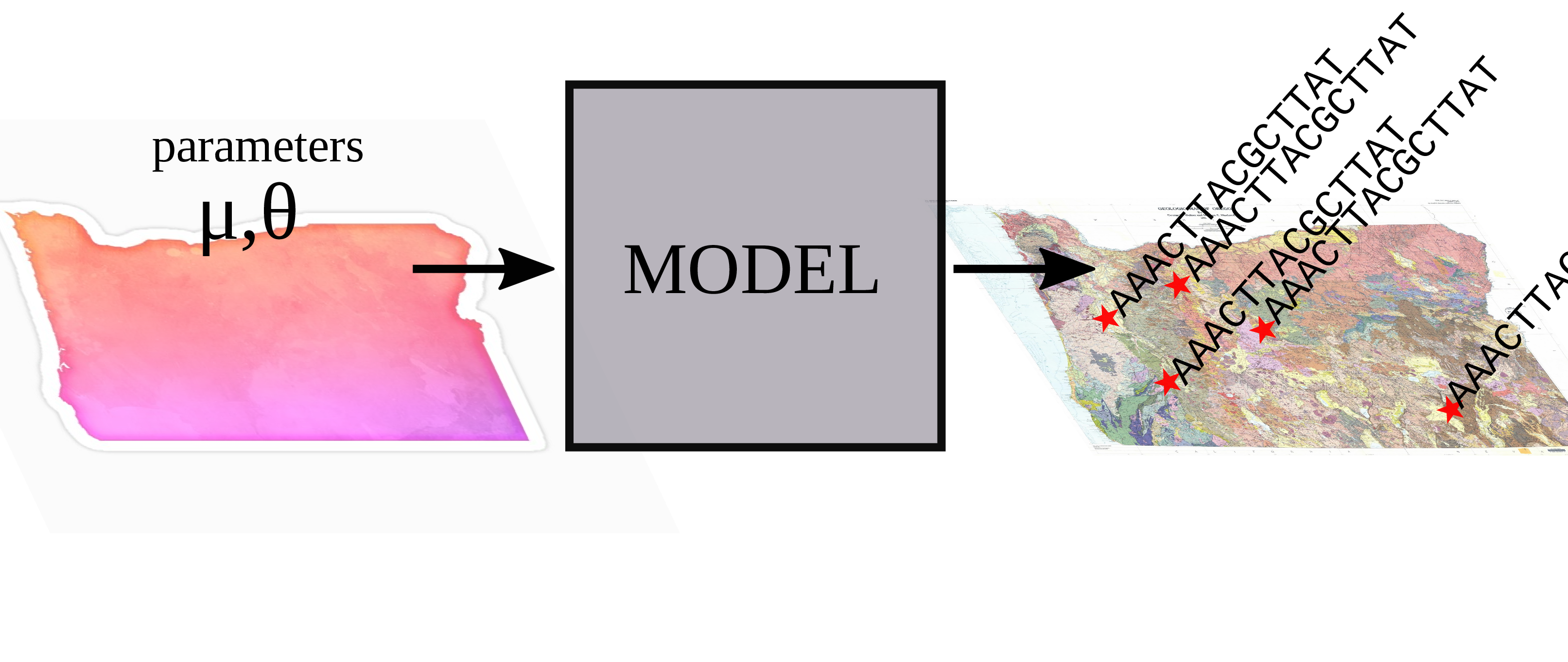
Inverse problems
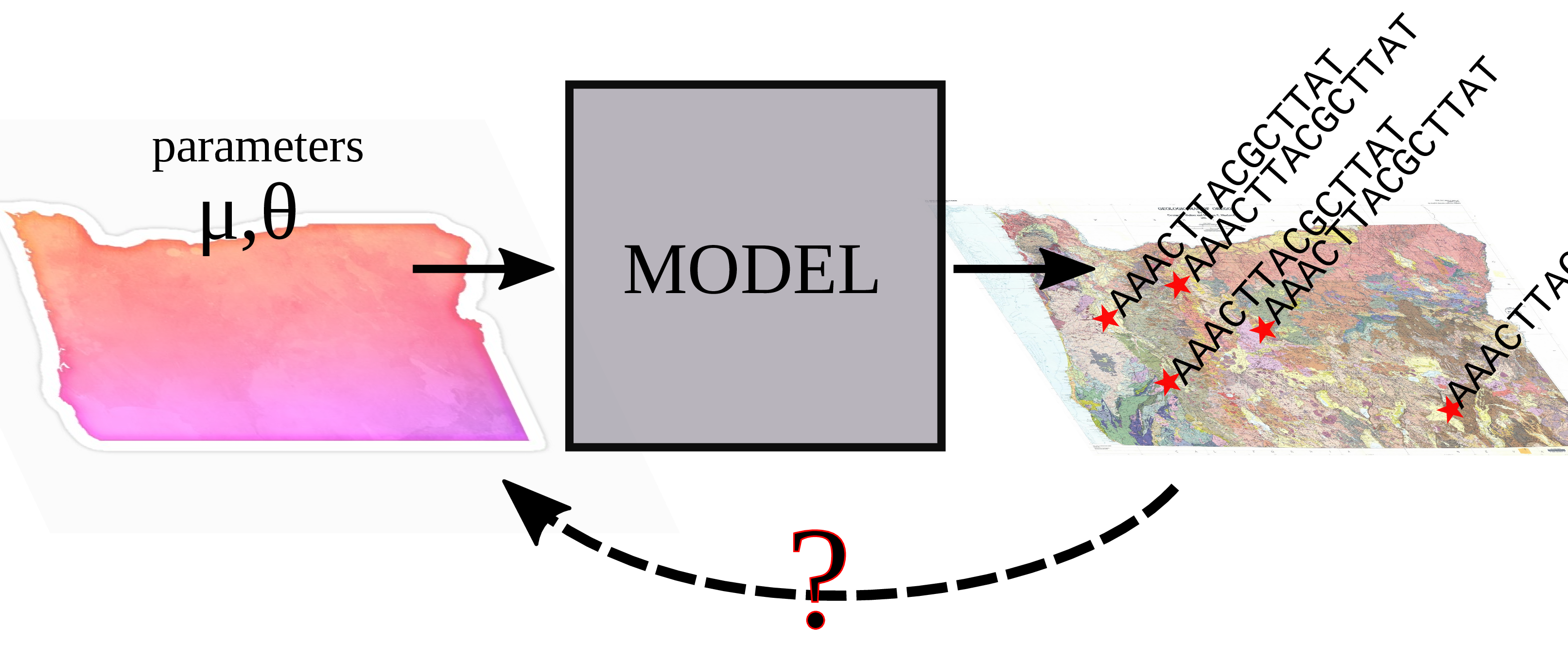
Inverse problems
Simulation-based inference

- bespoke confirmatory simulations
- optimization of one or two parameters
- machine learning predictors (e.g., random forests)
- Approximate Bayesian Computation (ABC)
- deep learning
What do we need
Wish list:
Whole genomes, thousands of samples,
from millions of individuals.
Demography:
- life history
- separate sexes
- selfing
- polyploidy
- species interactions
Geography:
- discrete populations
- continuous landscapes
- barriers
History:
- ancient samples
- range shifts
Natural selection:
- selective sweeps
- introgressing alleles
- background selection
- quantitative traits
- incompatibilities
- local adaptation
Genomes:
- recombination rate variation
- gene conversion
- infinite-sites mutation
- nucleotide models
- context-dependence
- mobile elements
- inversions
- copy number variation
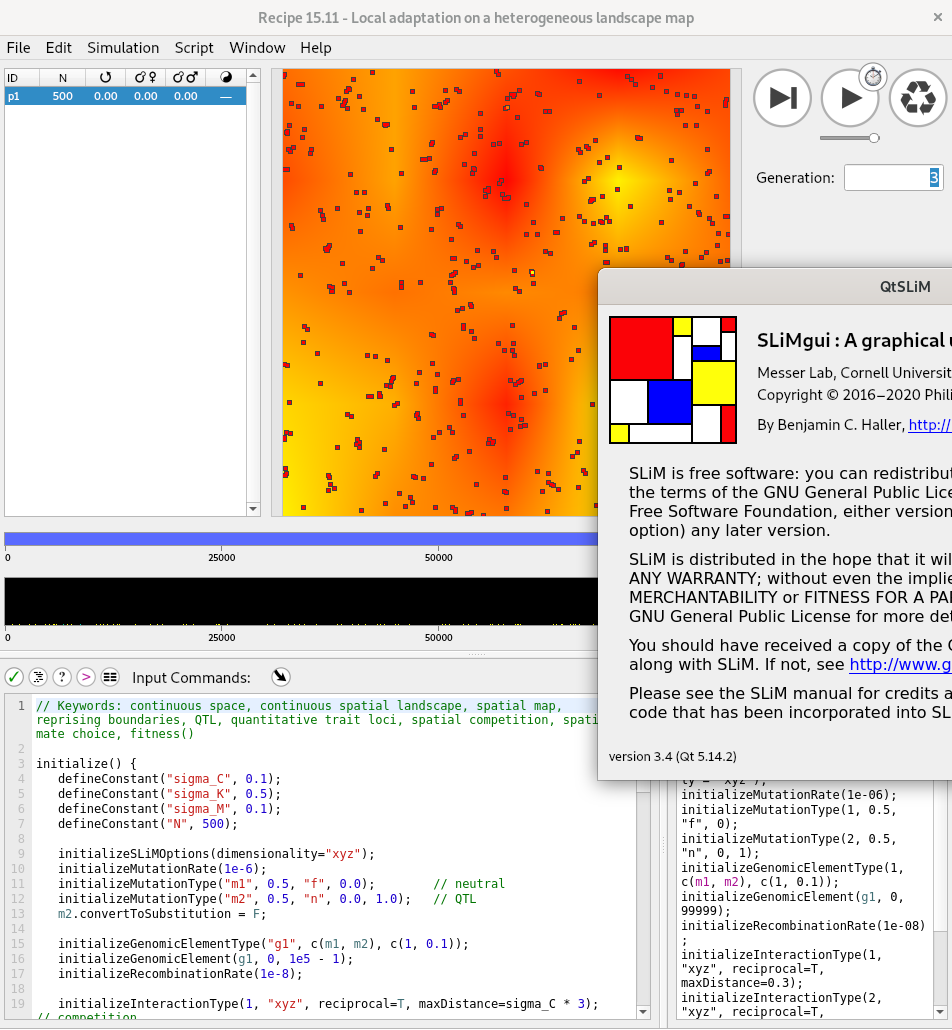
Enter SLiM
by Ben Haller and Philipp Messer
- a forwards simulator
- arbitary life cycles
- continuous geography and local interactions
- quantitative traits
- anything is possible
 Ben Haller
Ben Haller
Whole genomes,*thousands of samples,from millions of individuals.*
Demography:
life historyseparate sexes*selfing- polyploidy*
- species interactions (coming soon!)
Geography:
discrete populationscontinuous landscapesbarriers*
History:
ancient samplesrange shifts
Natural selection:
selective sweepsintrogressing allelesbackground selectionquantitative traits*incompatibilities*local adaptation*
Genomes:
recombination rate variationgene conversioninfinite-sites mutationnucleotide modelscontext-dependence*- mobile elements*
- inversions*
- copy number variation
Whole genomes,*
Idea: if we record how everyone is related to everyone else,
we can put down neutral mutations after the simulation is over instead of carrying them along.
Since neutral mutations don’t affect demography,
this is equivalent to having kept track of them throughout.
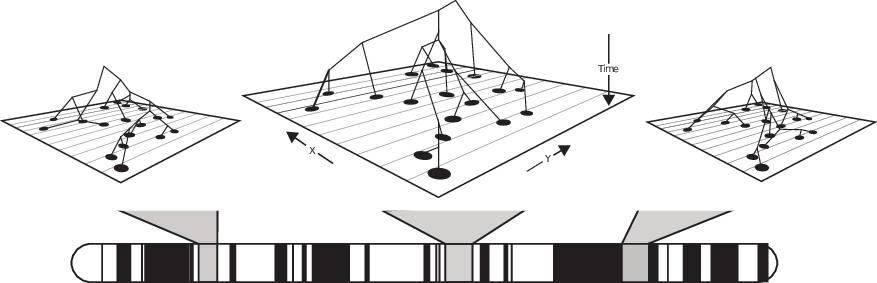
The tree sequence
History is a sequence of trees
For a set of sampled chromosomes, at each position along the genome there is a genealogical tree that says how they are related.
The succinct tree sequence
is a way to succinctly describe this, er, sequence of trees
and the resulting genome sequences.


jerome kelleher
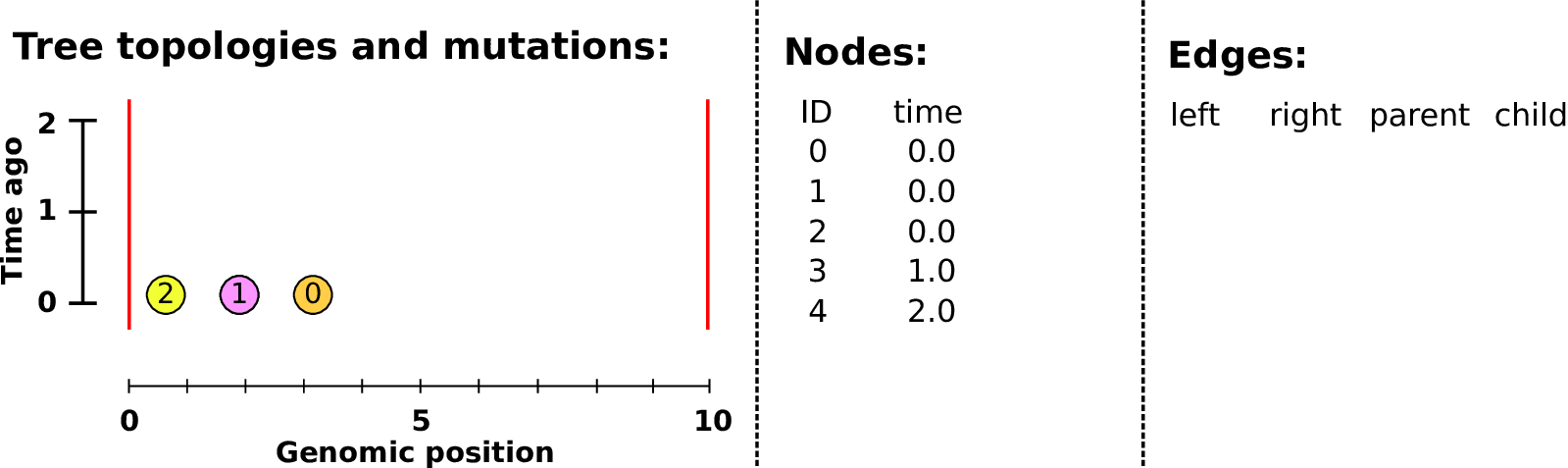
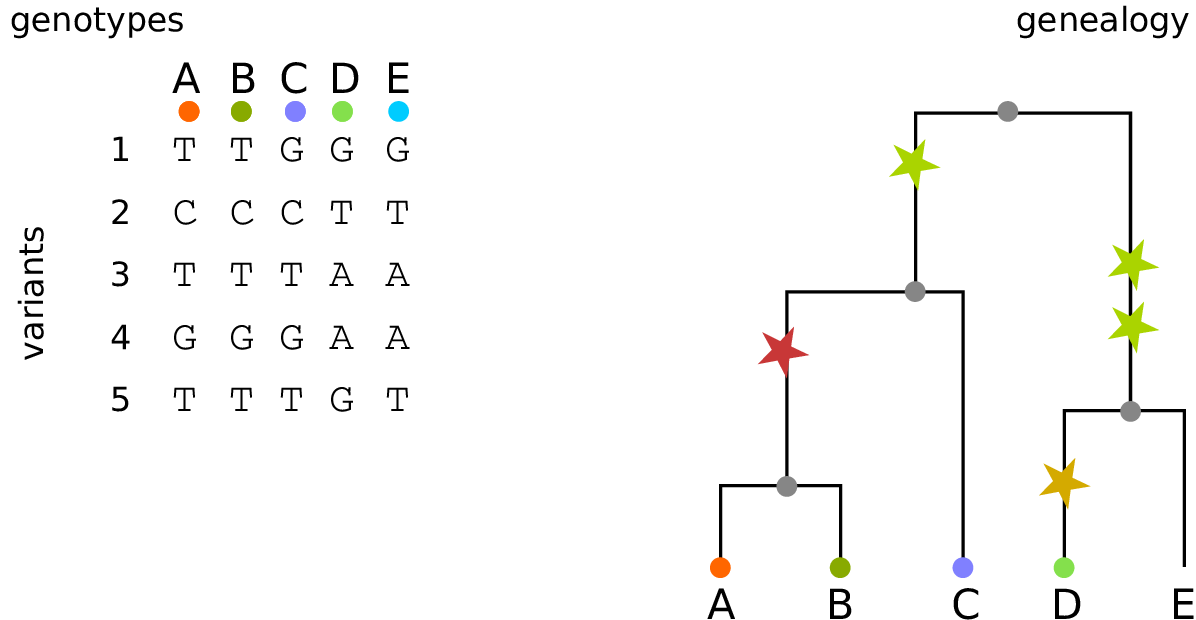
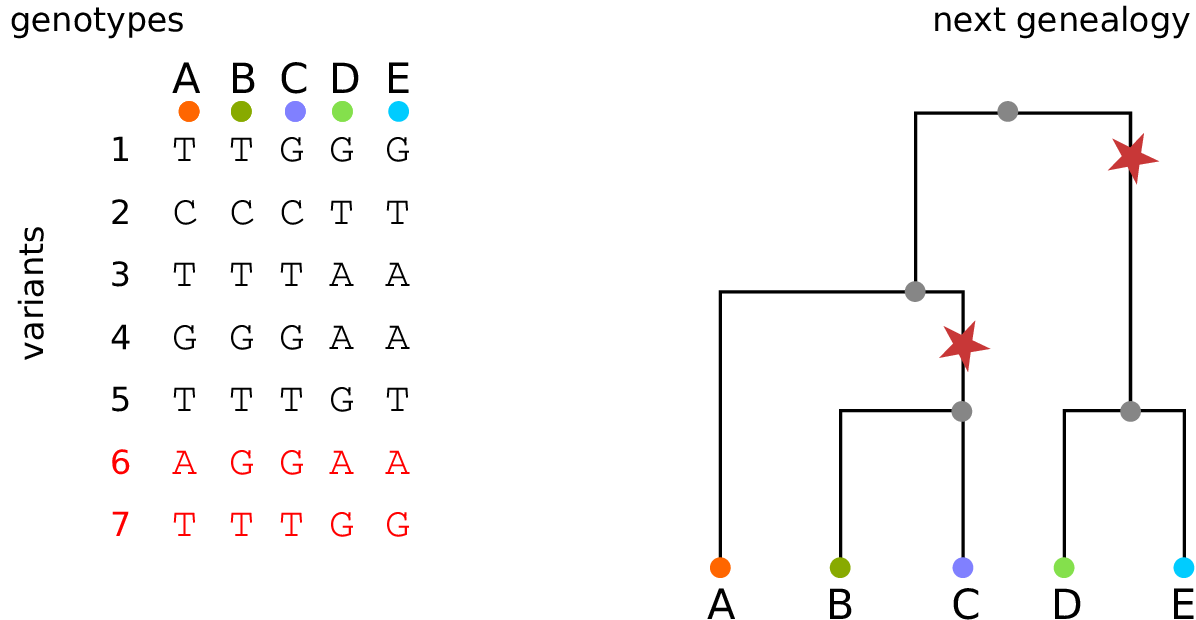
Example: three samples; two trees; two variant sites
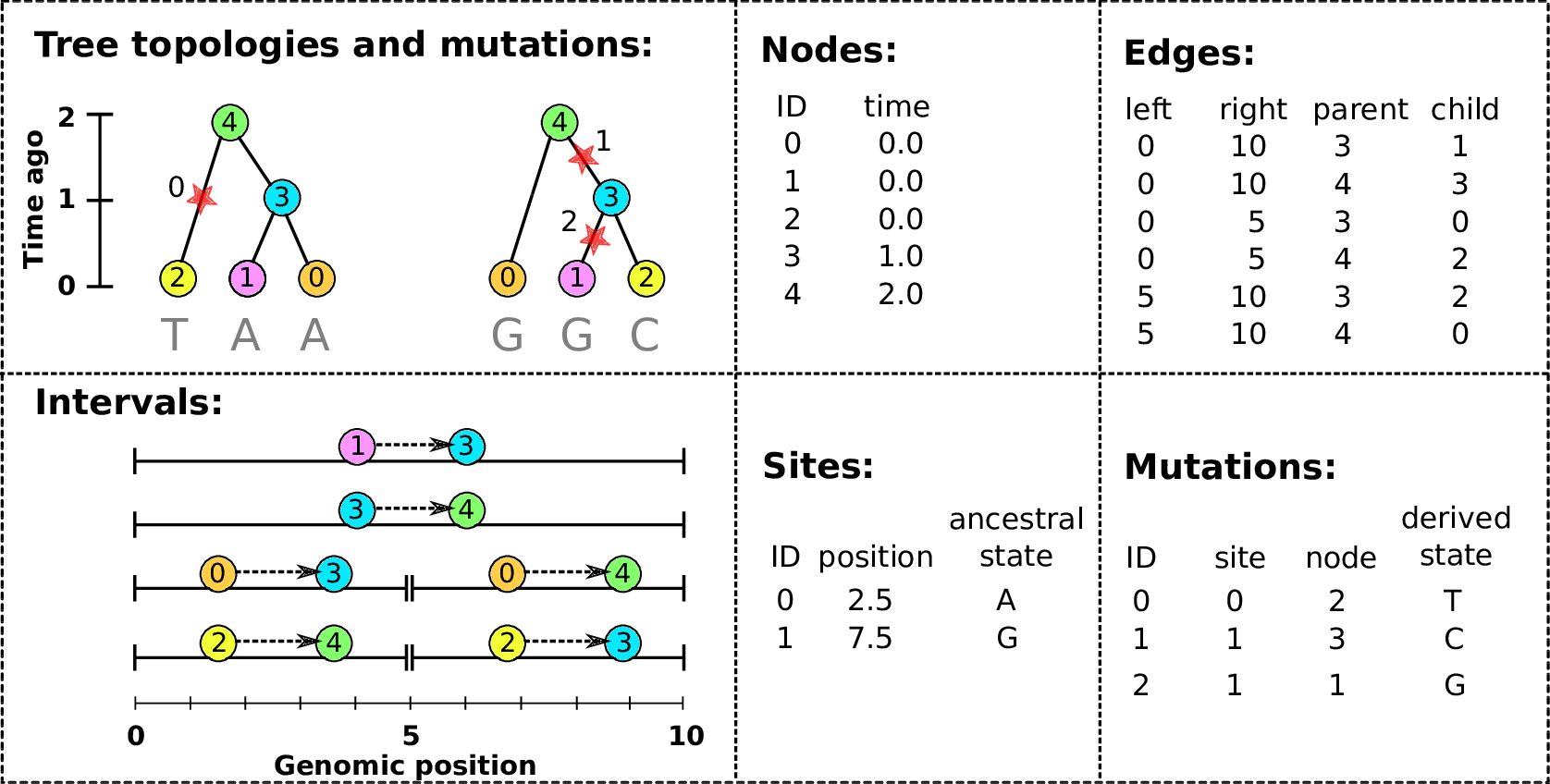
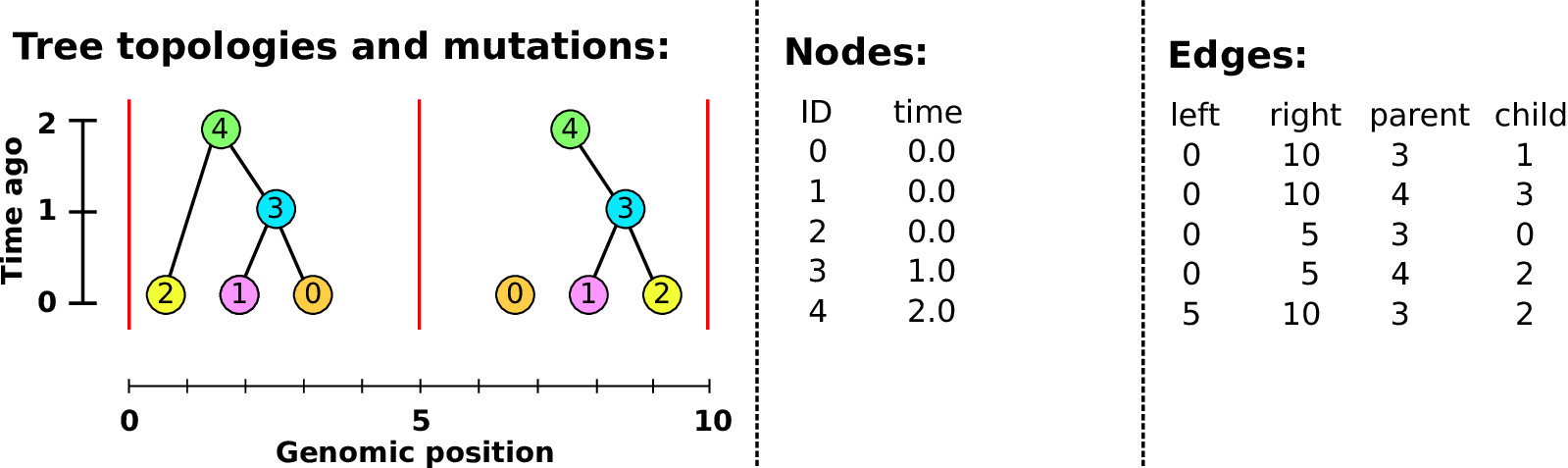
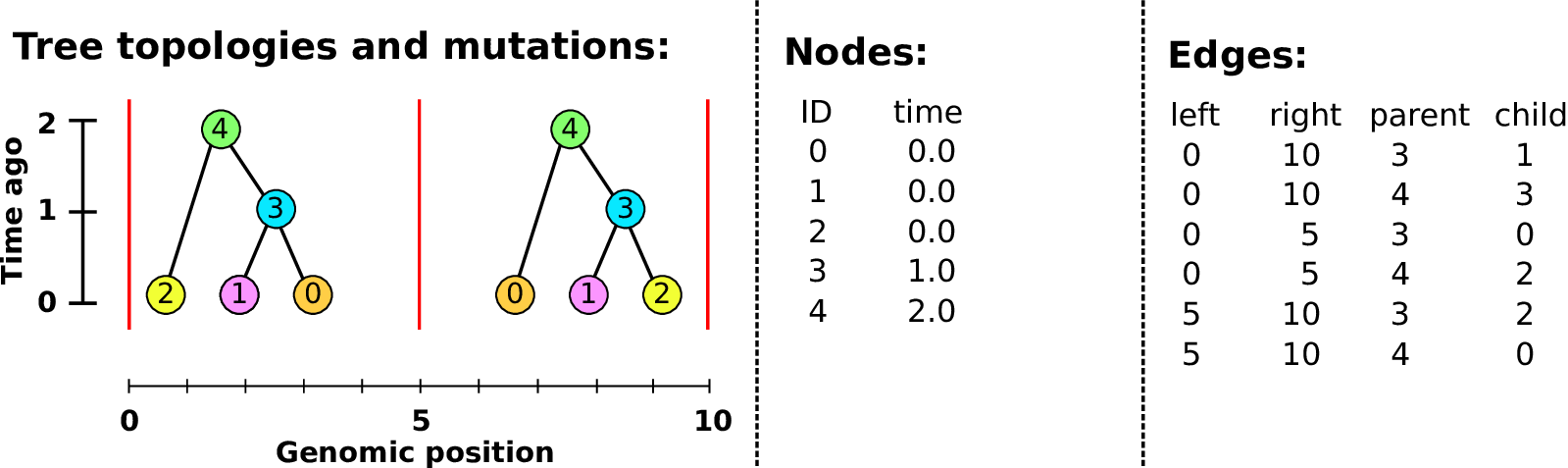
Nodes and edges
- Edges
Who inherits from who.
Records: interval (left, right); parent node; child node.
- Nodes
The ancestors those happen in.
Records: time ago (of birth); ID (implicit).
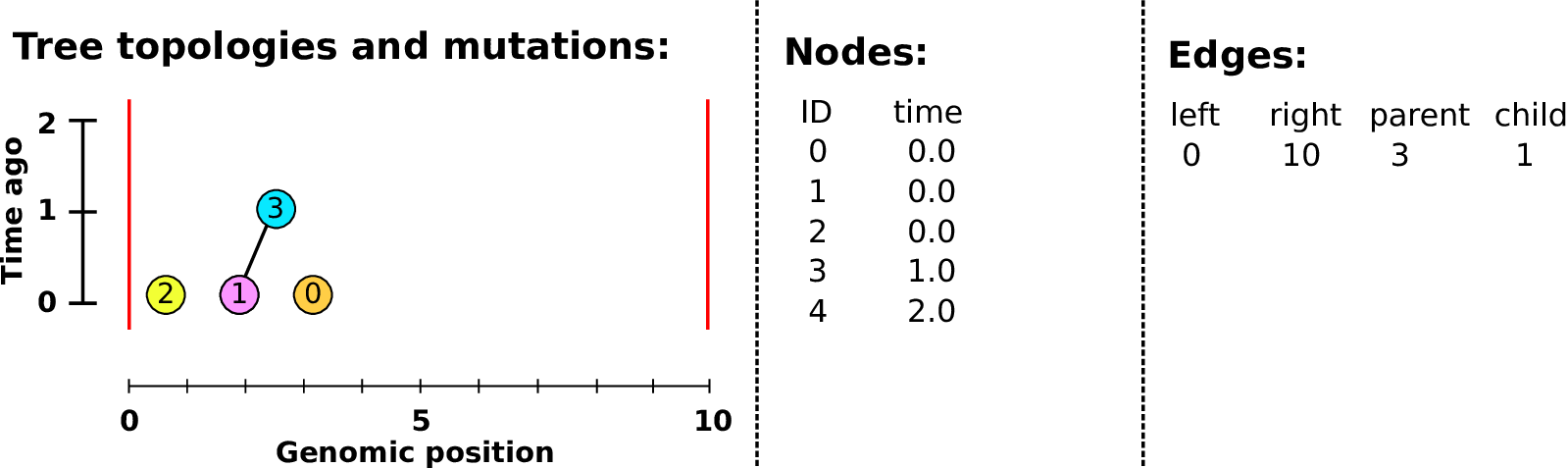
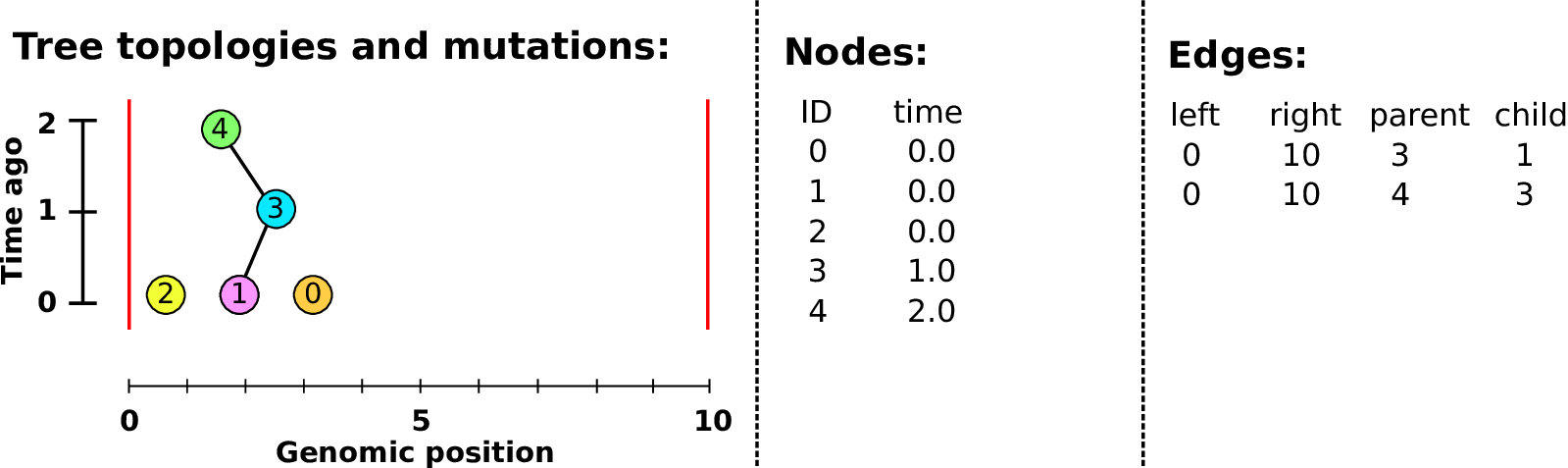
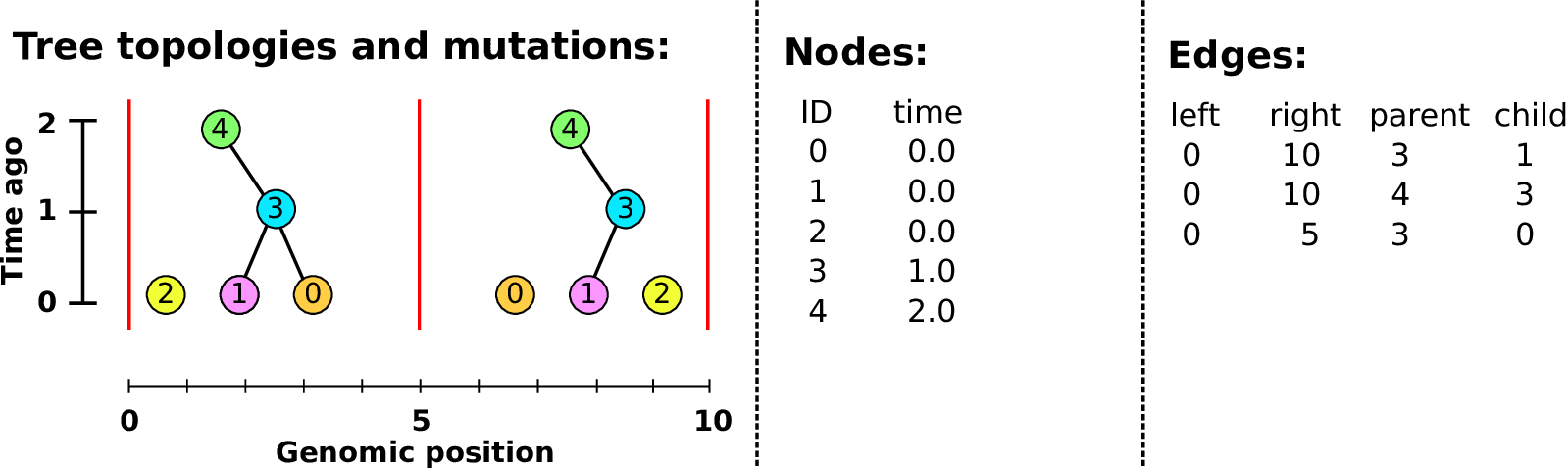
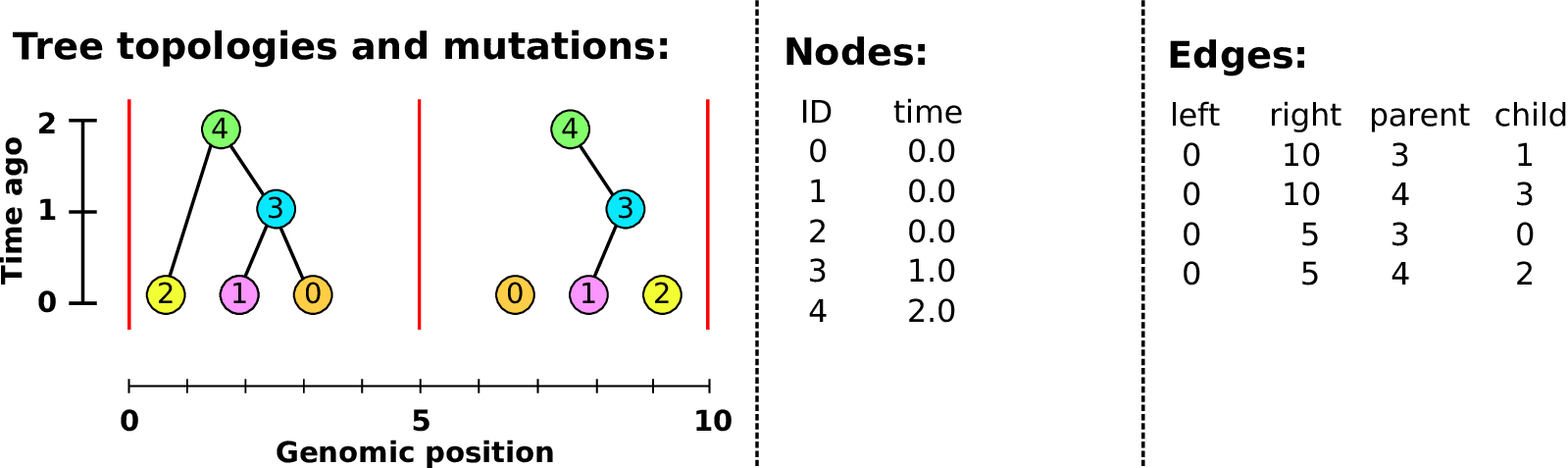
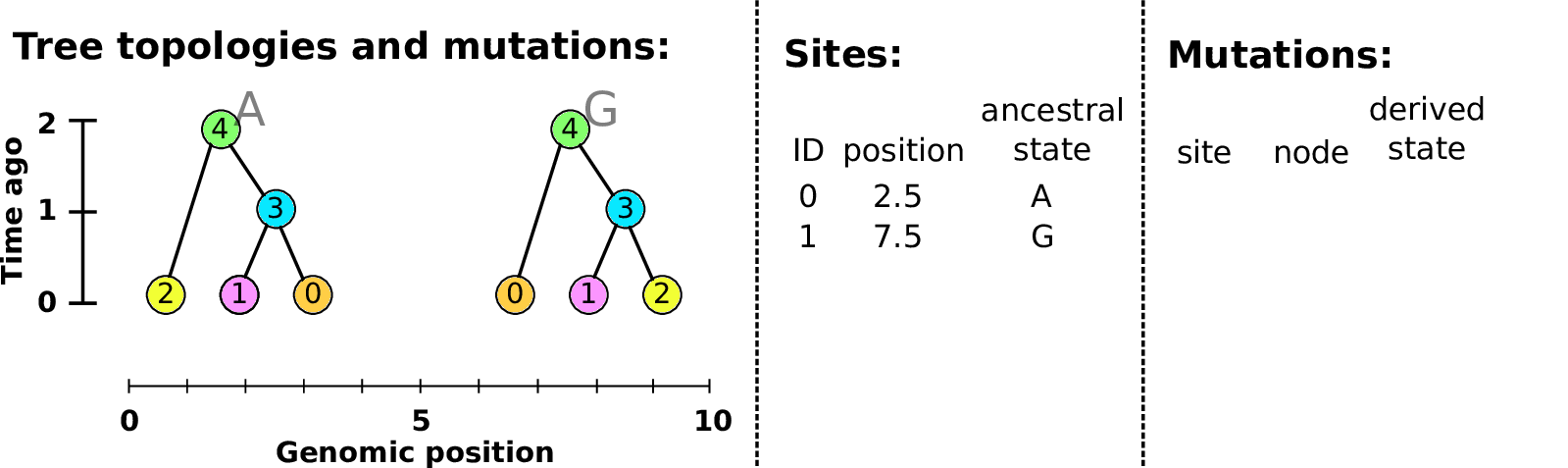
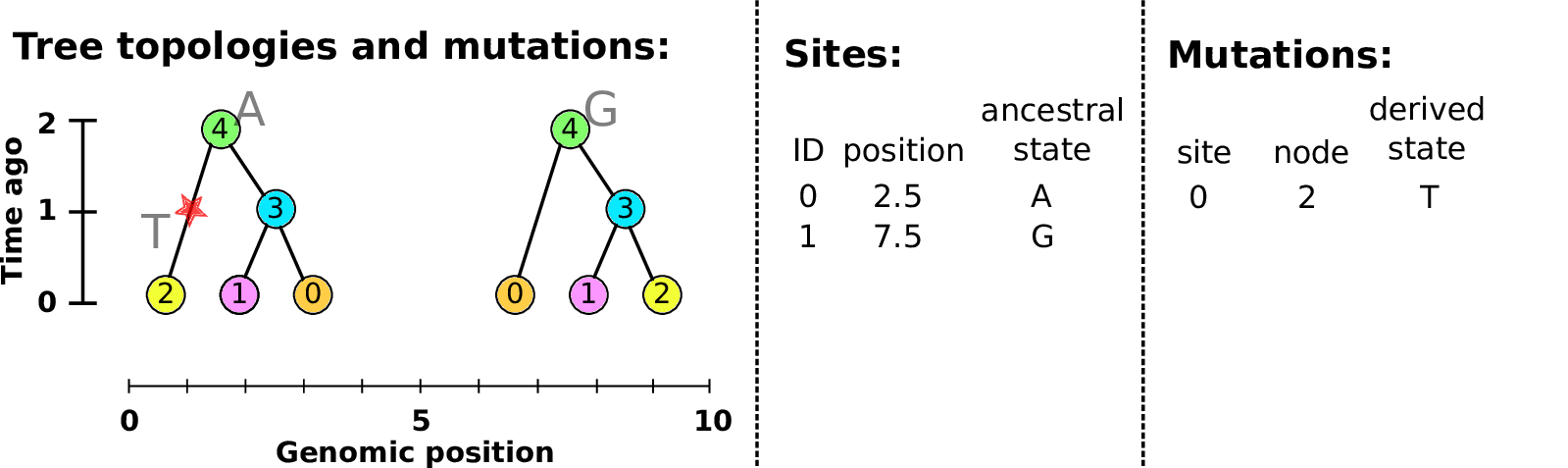
Sites and mutations
- Mutations
When state changes along the tree.
Records: site it occured at; node it occurred in; derived state.
- Sites
Where mutations fall on the genome.
Records: genomic position; ancestral (root) state; ID (implicit).
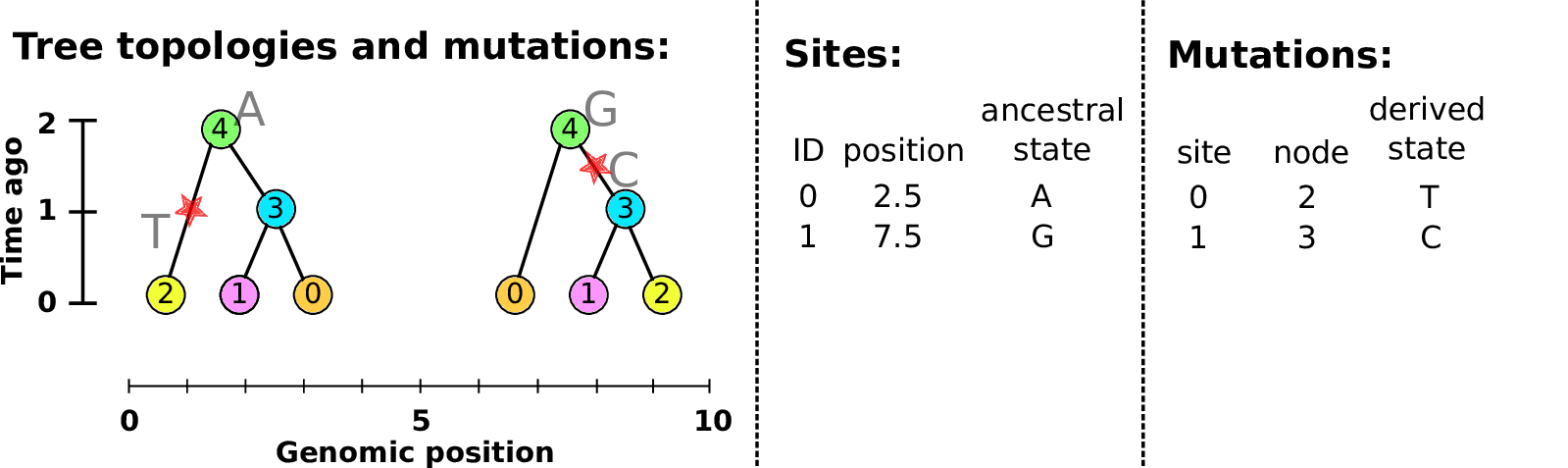
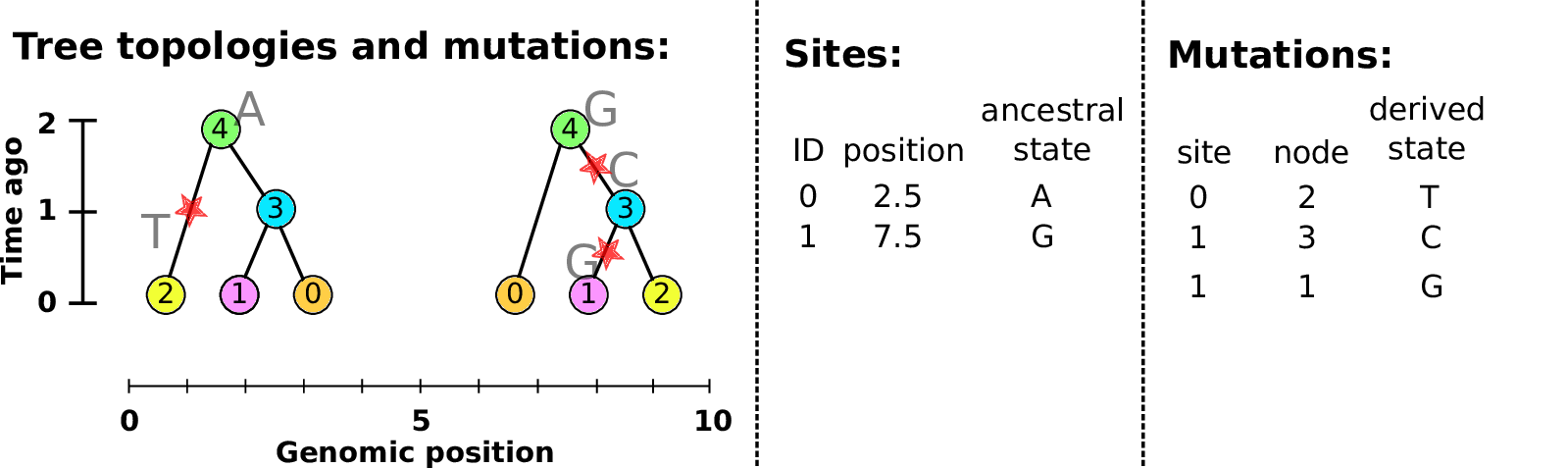
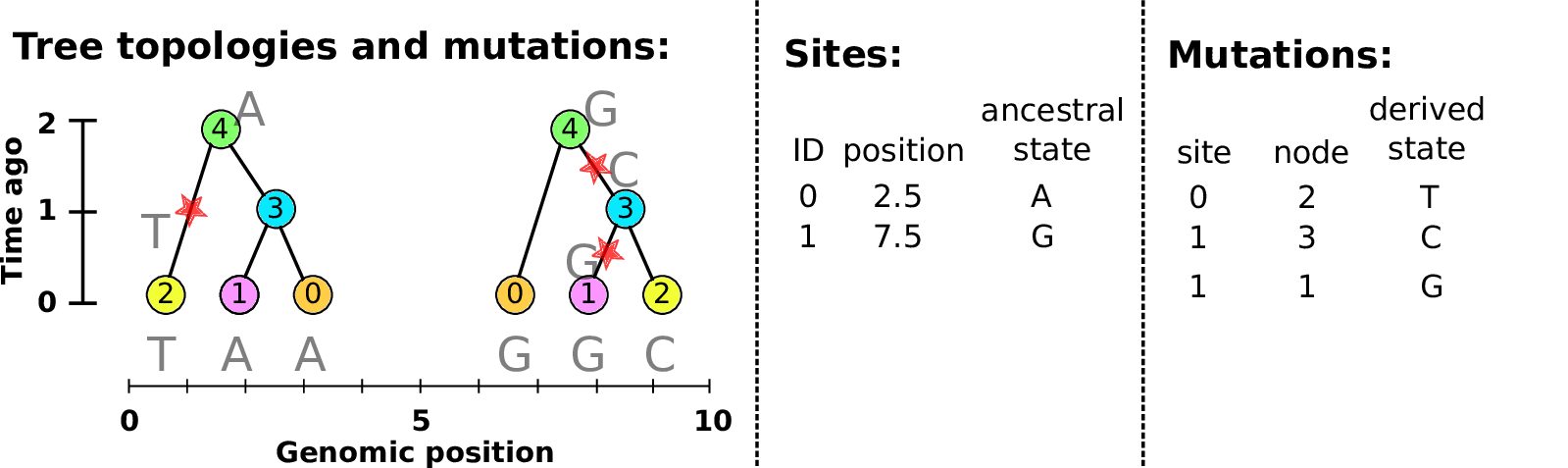
The result: an encoding of the genomes and all the genealogical trees.

How’s it work?
File sizes
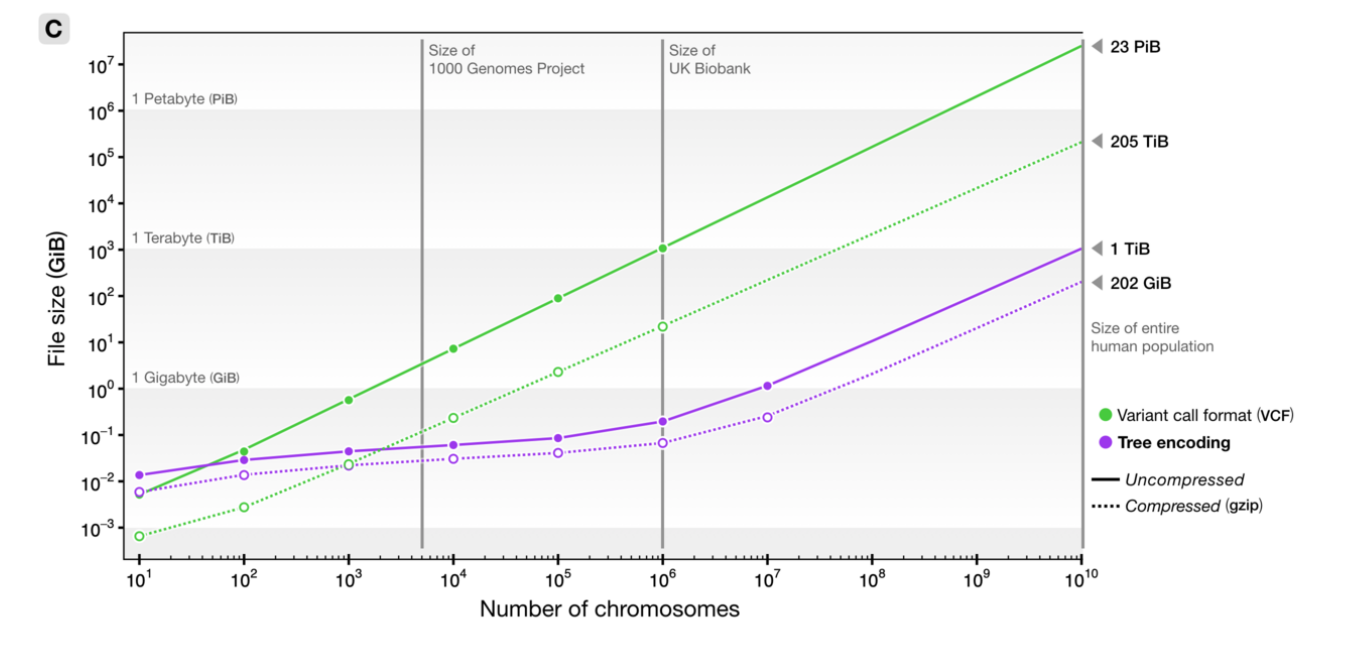
100Mb chromosomes; from Kelleher et al 2018, Inferring whole-genome histories in large population datasets, Nature Genetics
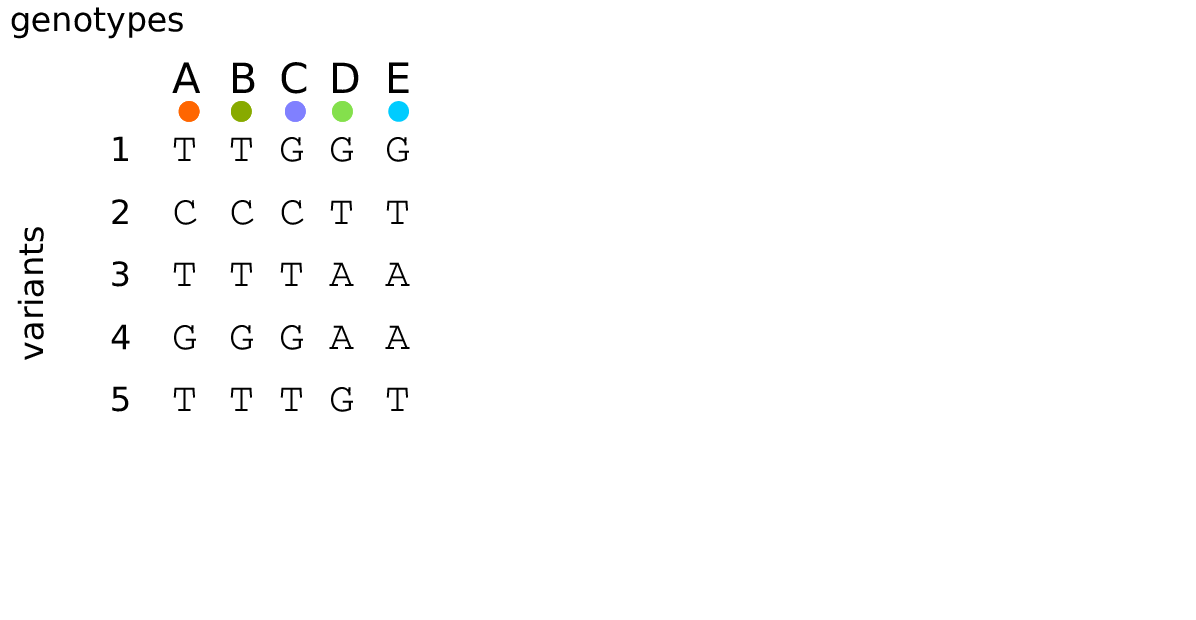
For \(N\) samples genotyped at \(M\) sites
Genotype matrix:
\(N \times M\) things.
Tree sequence:
- \(2N-2\) edges for the first tree
- \(\sim 4\) edges per each of \(T\) trees
- \(M\) mutations
\(O(N + T + M)\) things

Fast genotype statistics, too!
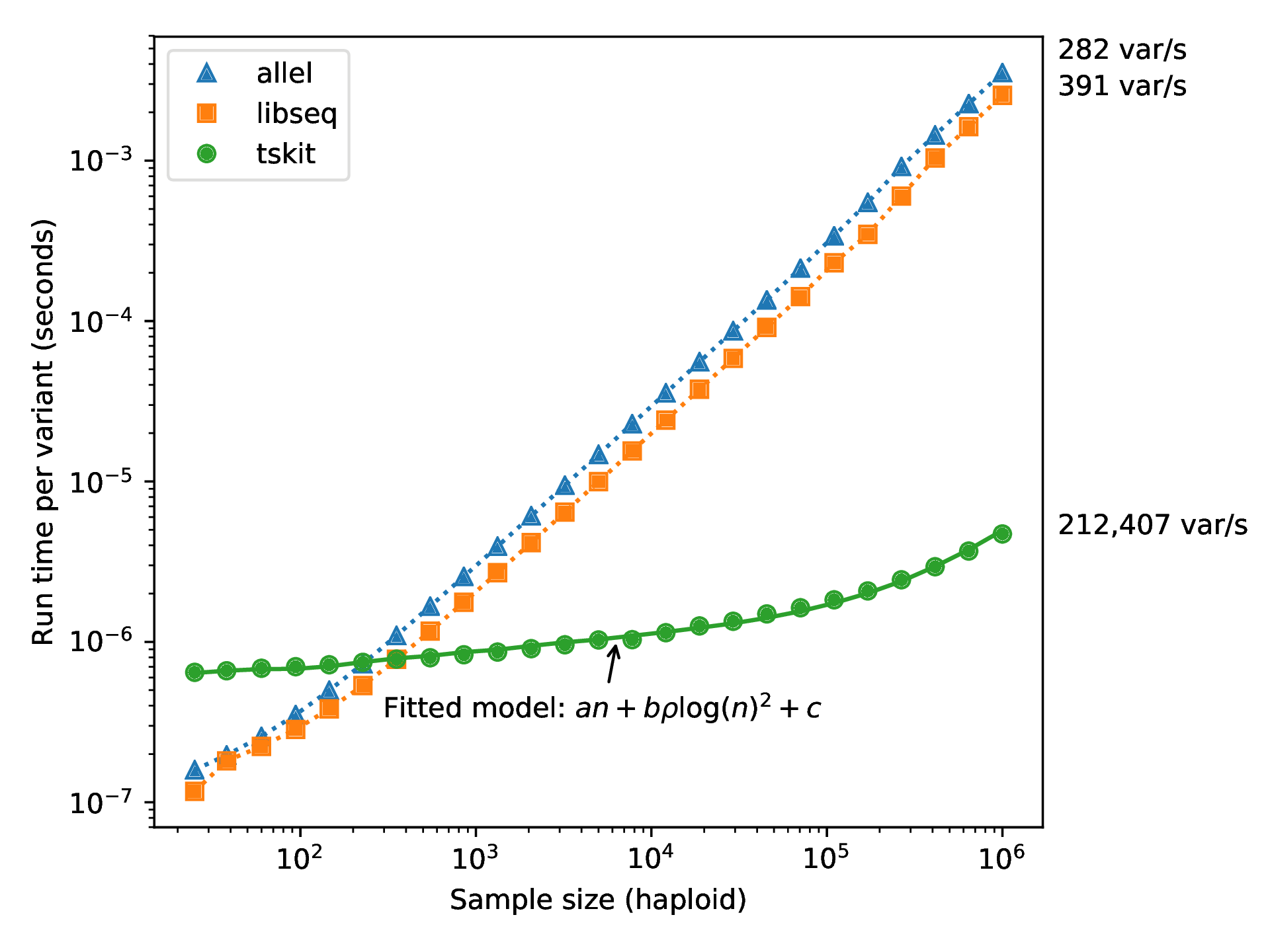
from Ralph, Thornton and Kelleher 2019, Efficiently summarizing relationships in large samples
Application to genomic simulations
The main idea
If we record the tree sequence that relates everyone to everyone else,
after the simulation is over we can put neutral mutations down on the trees.
Since neutral mutations don’t affect demography,
this is equivalent to having kept track of them throughout.
From Kelleher, Thornton, Ashander, and Ralph 2018, Efficient pedigree recording for fast population genetics simulation.
and Haller, Galloway, Kelleher, Messer, and Ralph 2018, Tree‐sequence recording in SLiM opens new horizons for forward‐time simulation of whole genomes



This means recording the entire genetic history of everyone in the population, ever.
It is not clear this is a good idea.
But, with a few tricks…
A 100x speedup!

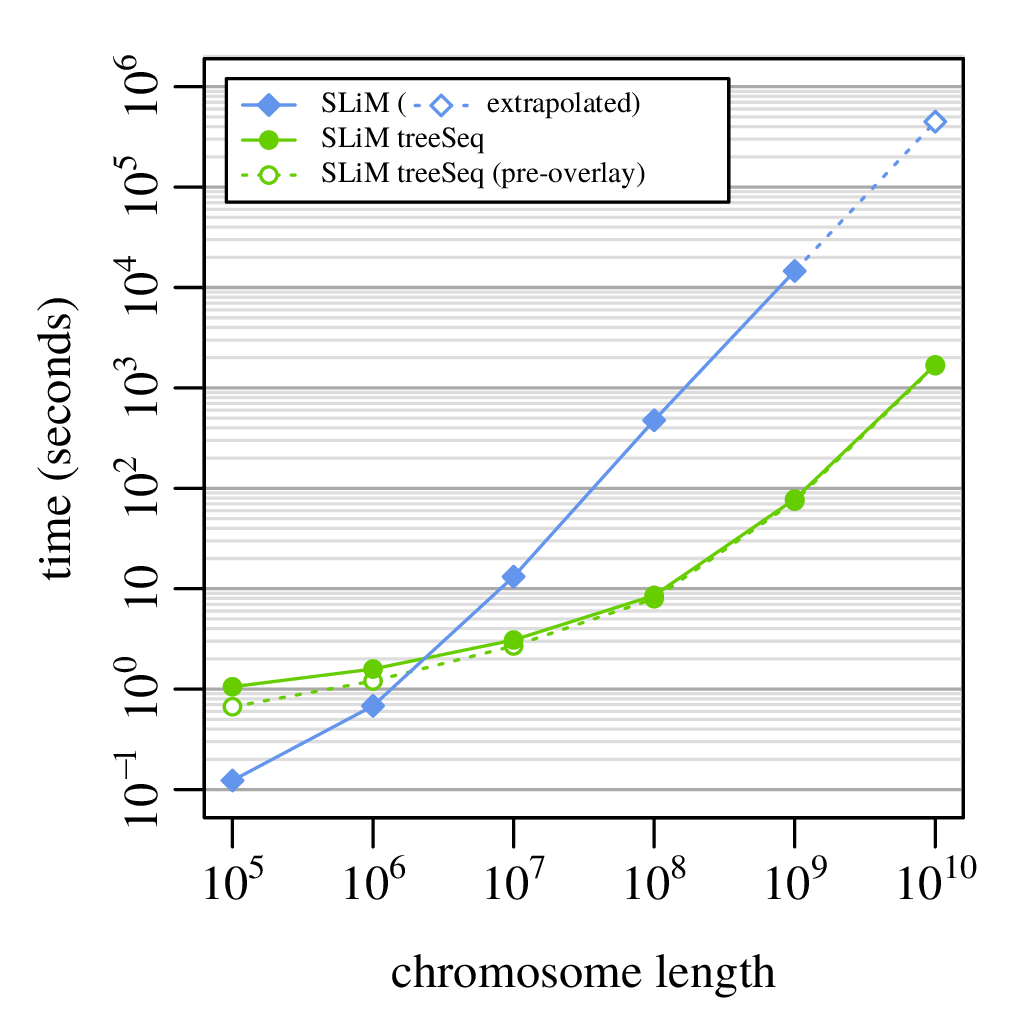
What else can you do with tree sequences?
- recorded pedigree and migration history
- true ancestry assignment
- recapitation: fast, post-hoc initialization with coalescent simulation
- fast, convenient computation
For example:
- genome as human chr7 (\(1.54 \times 10^8\)bp)
- \(\approx\) 10,000 diploids
- 500,000 overlapping generations
- continuous, square habitat
- selected mutations at rate \(10^{-10}\)
- neutral mutations added afterwards
Runtime: 8 hours
Example 1: landscapes of diversity
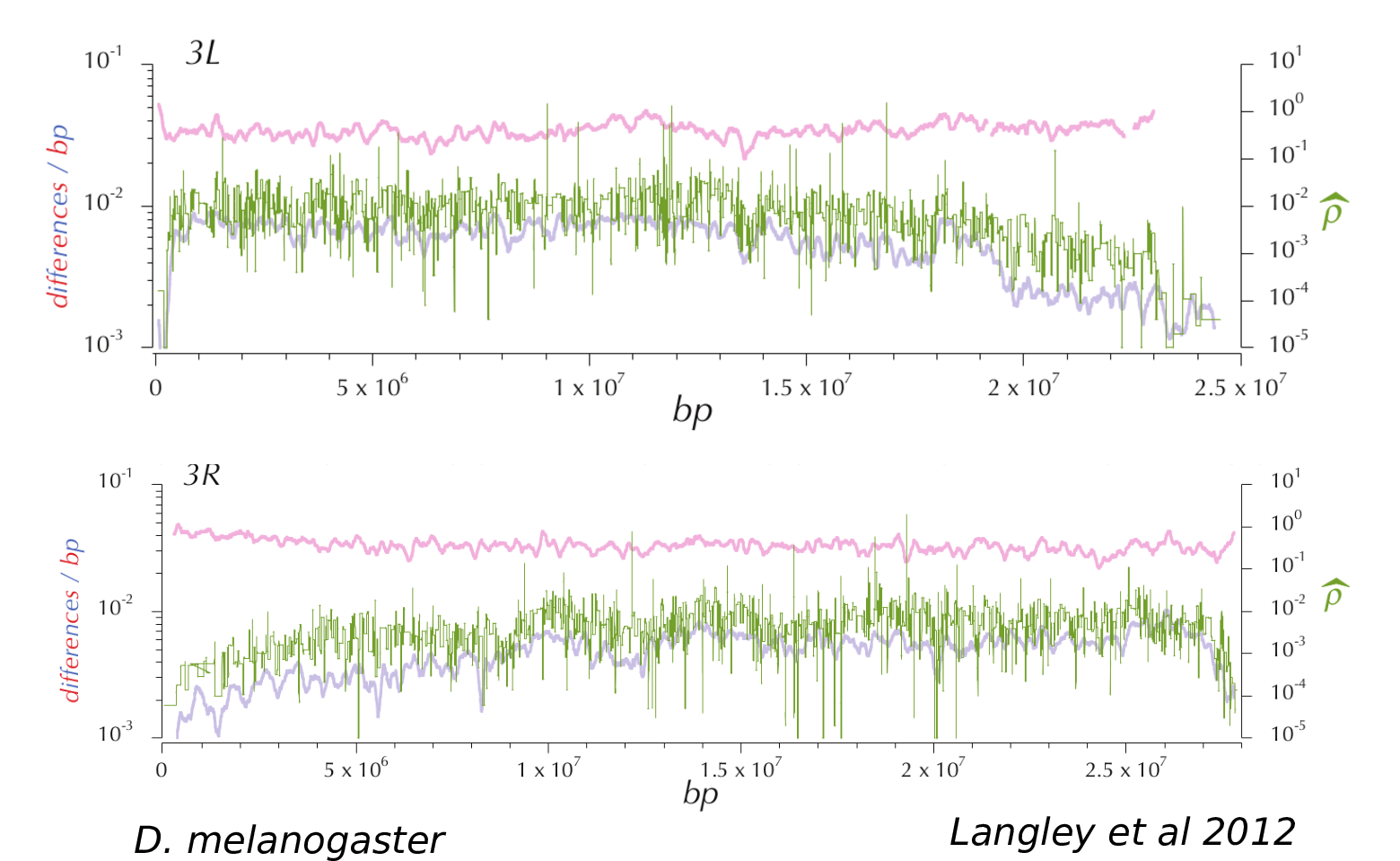
Diversity correlates with recombination rate
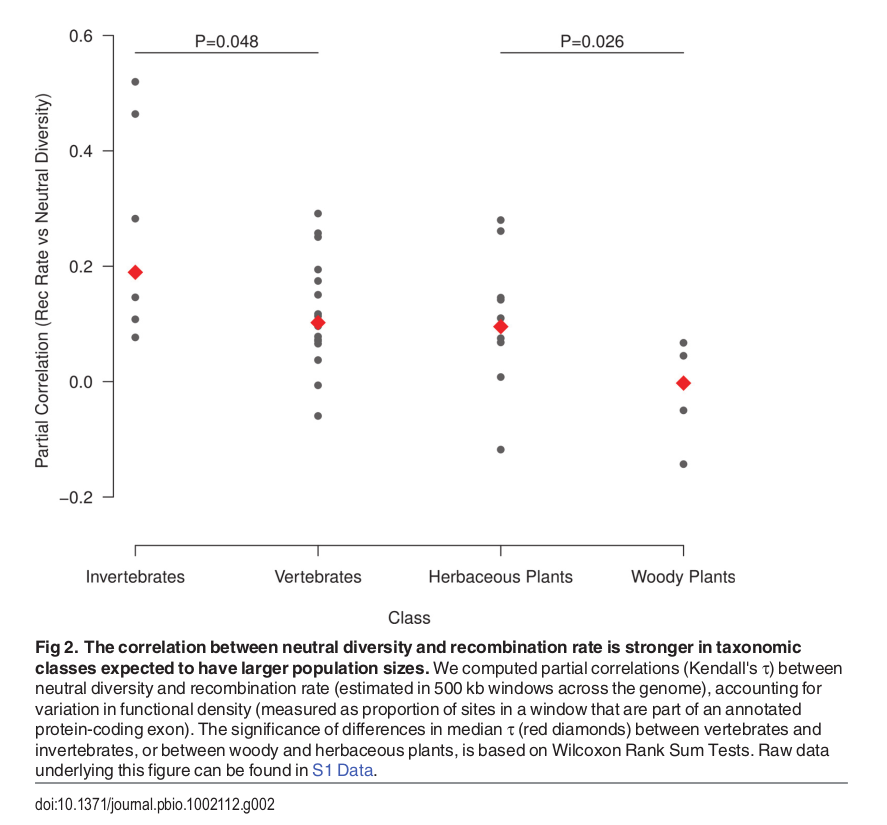
Hudson 1994; Cutter & Payseur 2013; Corbett-Detig et al 2015
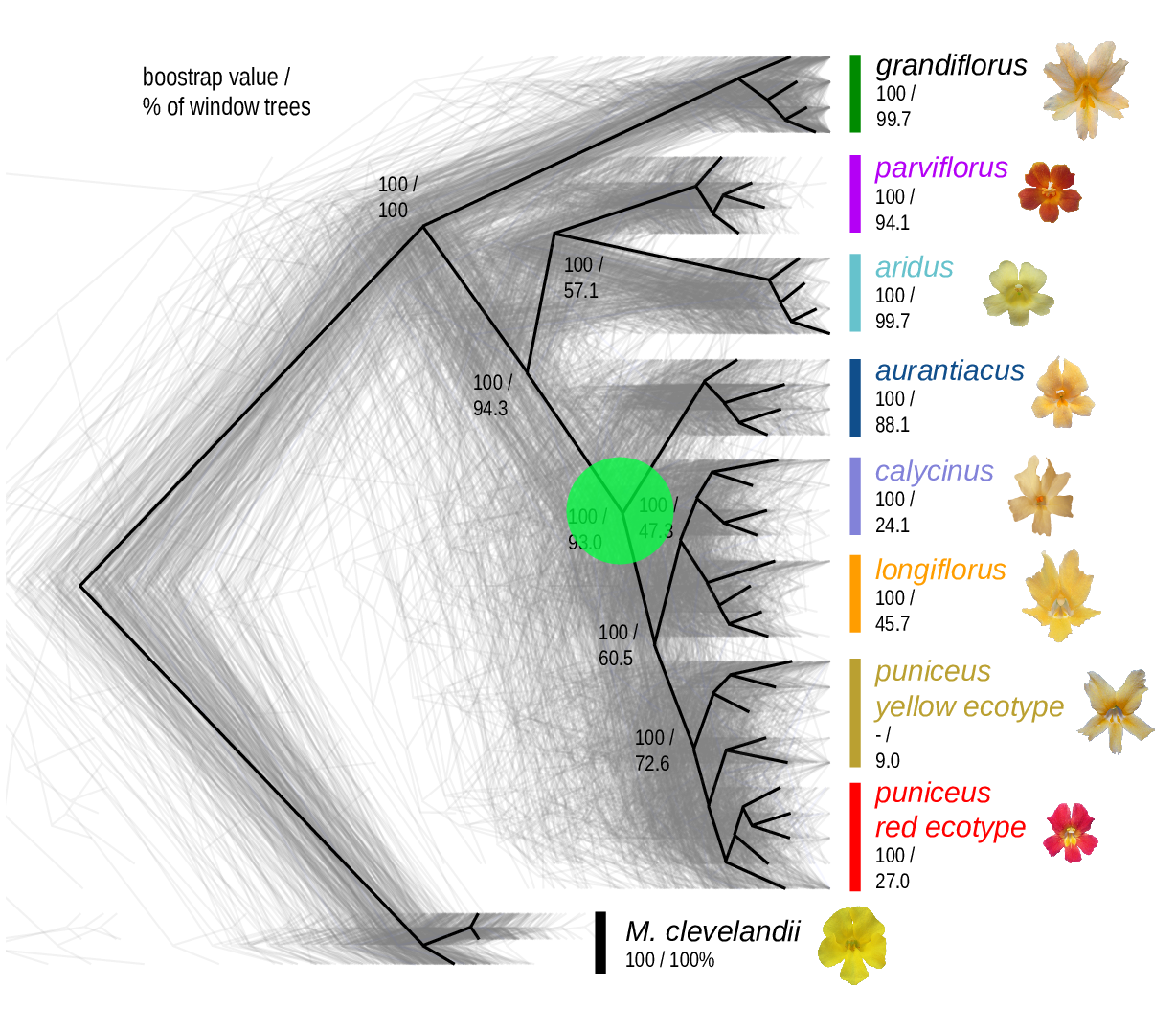
The Mimulus aurantiacus species complex
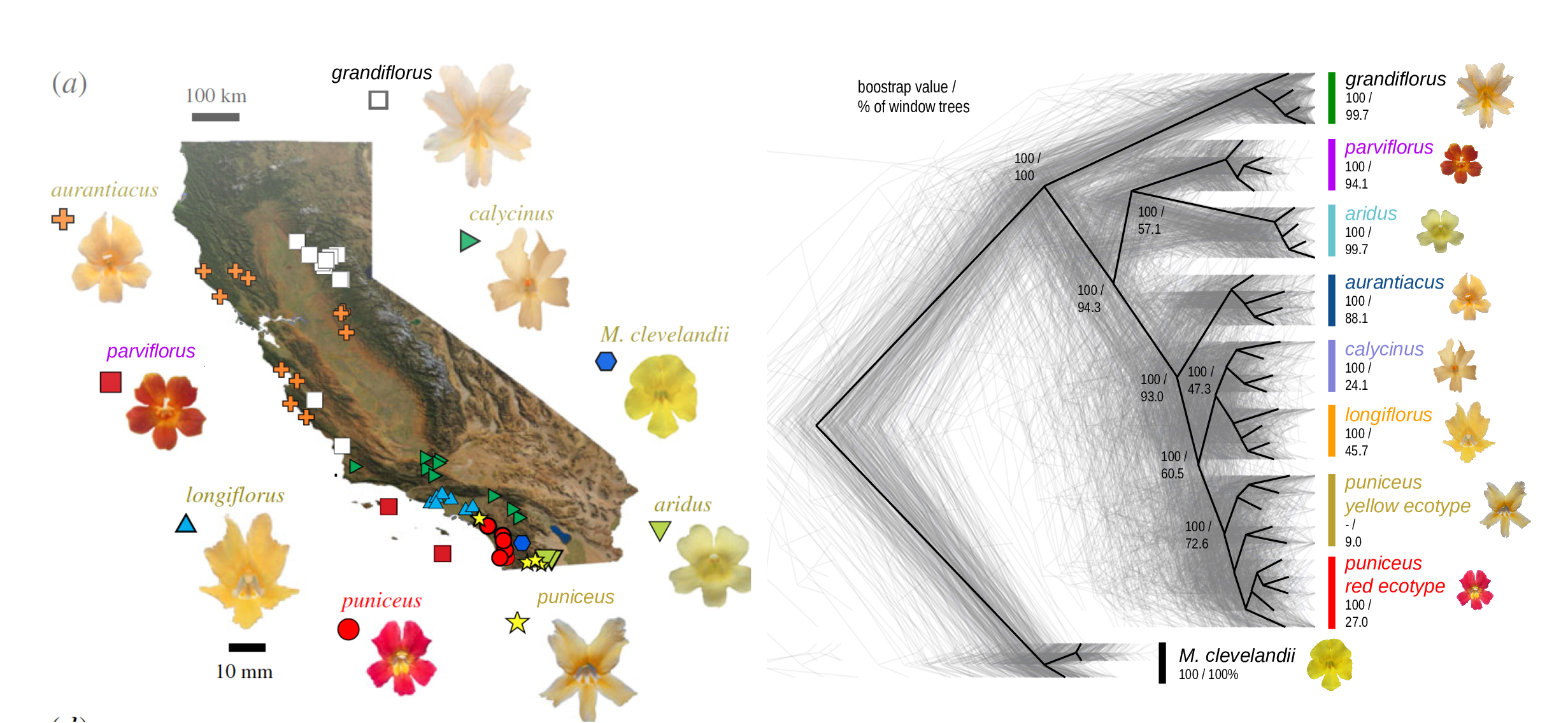
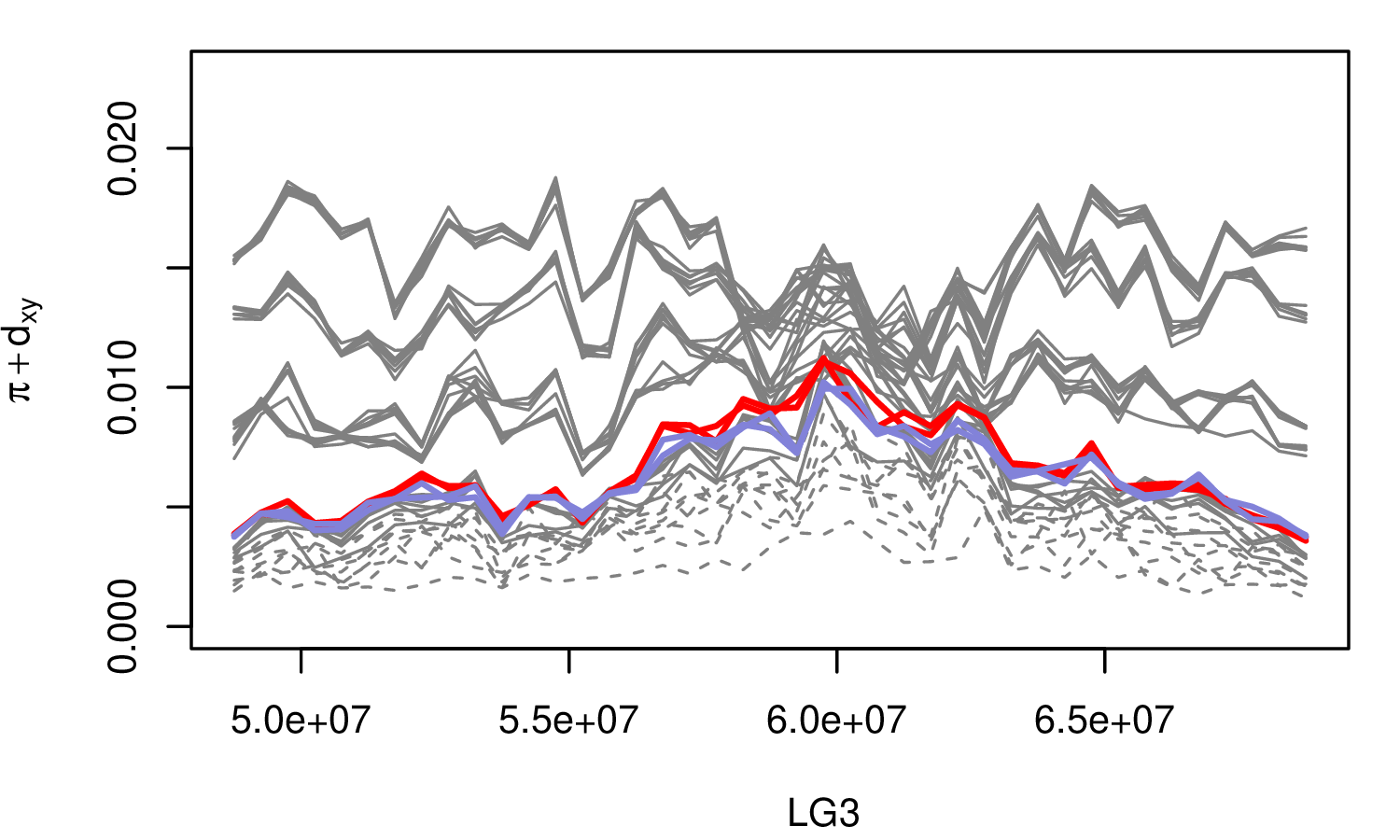
Simulations
\(N=10,000\) diploids
burn-in for \(10N\) generations
population split, with either:
- neutral
- background selection
- selection against introgressed alleles
- positive selection
- local adaptation

Murillo Rodrigues
From Widespread selection and gene flow shape the genomic landscape during a radiation of monkeyflowers, Stankowski, Chase, Fuiten, Rodrigues, Ralph, and Streisfeld; PLoS Bio 2019.
Conclusions:
neutralbackground selectionselection against introgressed alleles- positive selection
- local adaptation
From Widespread selection and gene flow shape the genomic landscape during a radiation of monkeyflowers, Stankowski, Chase, Fuiten, Rodrigues, Ralph, and Streisfeld; PLoS Bio 2019.
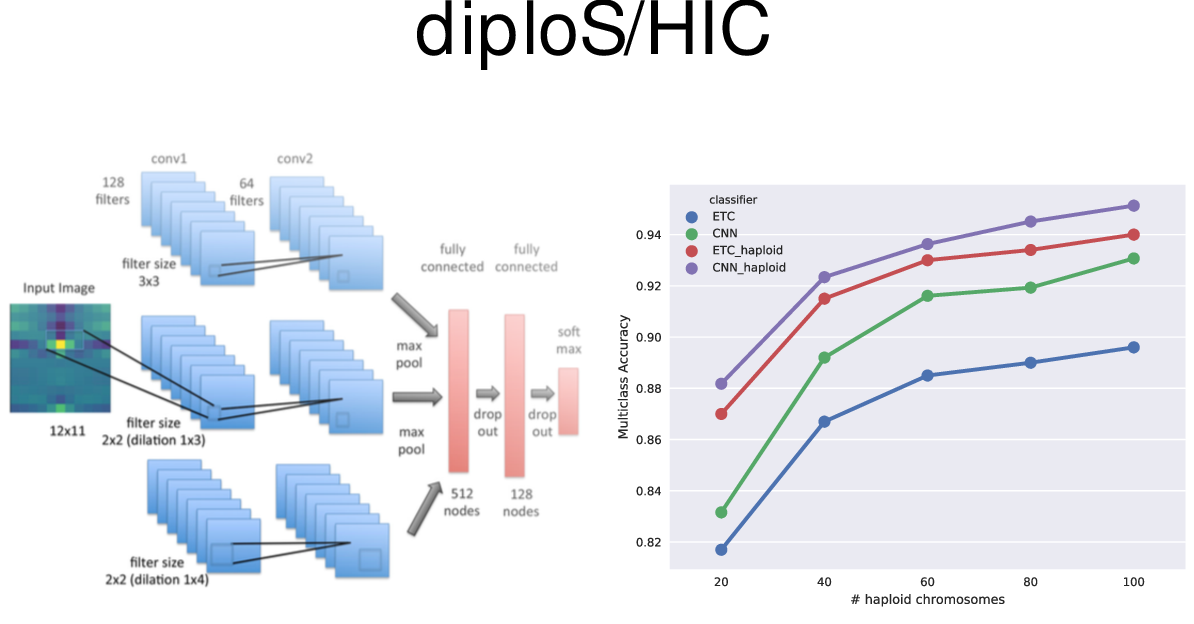
Example 2: identifying sweeps

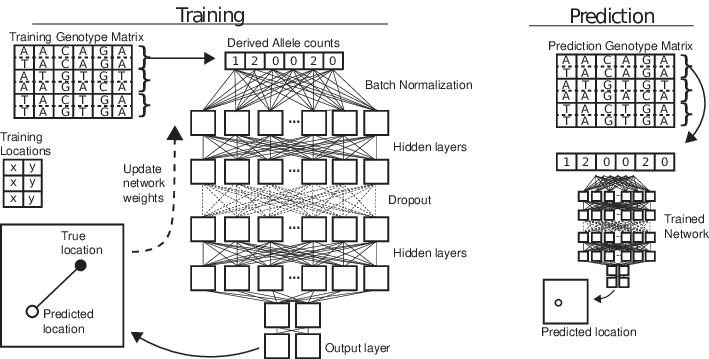
Example 3: predicting location
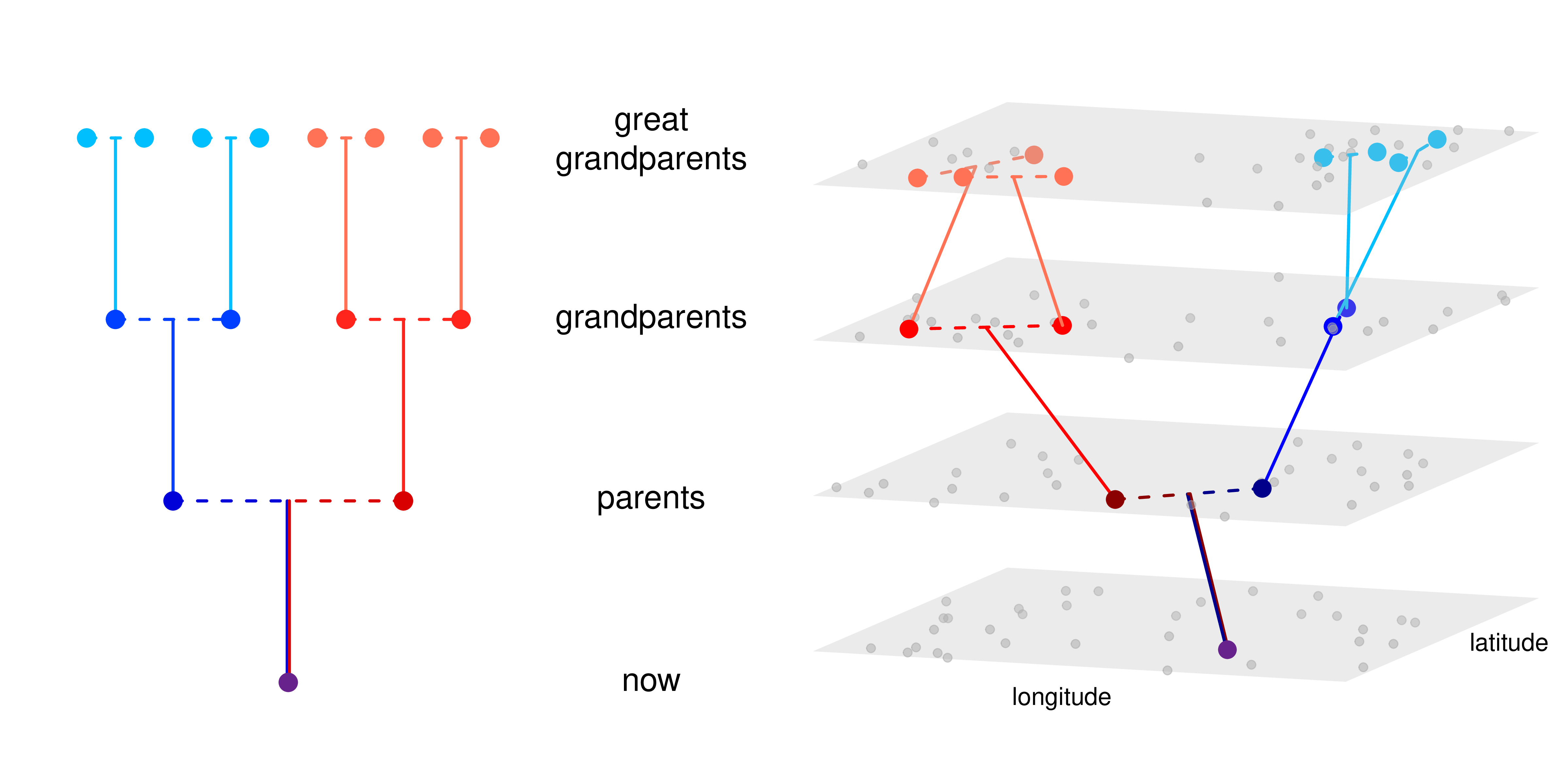
locator (Battey et al 2020)
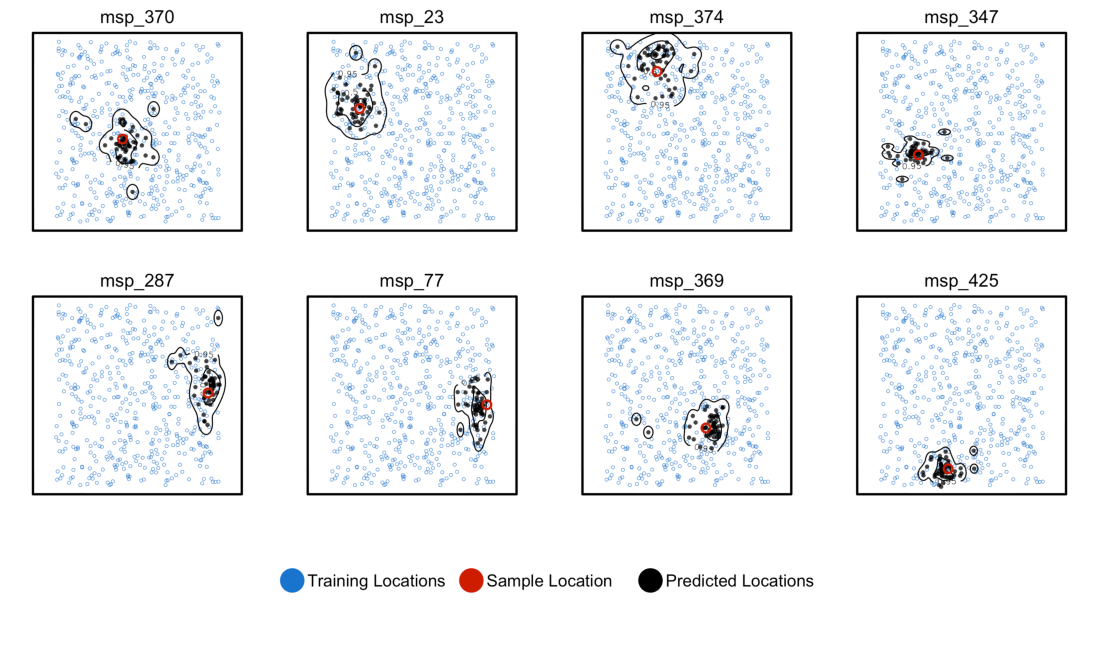
from Battey et al 2020
Example 4: dispersal maps
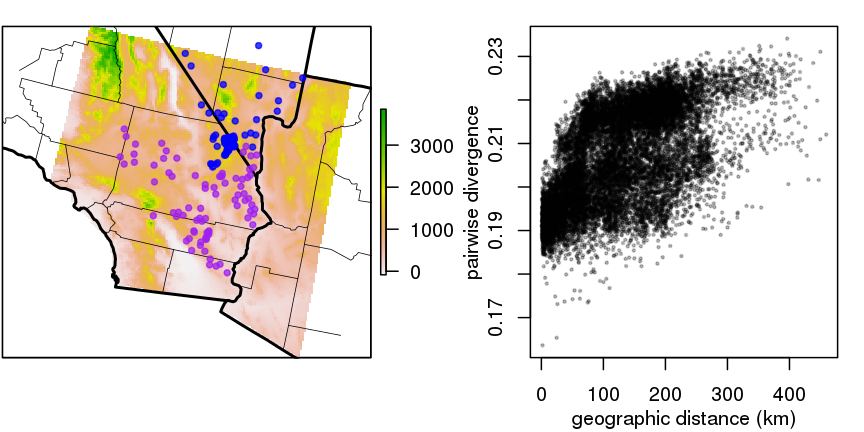
- genetic versus geographic distance between pairs of 272 desert tortoises (McCartney-Melstad, Shaffer)
- clouds are comparisons within/between the two colors
Wrap-up
Software development goals
- open
- welcoming and supportive
- reproducible and well-tested
- backwards compatible
- well-documented
- capacity building

Thanks!
- Andy Kern
- Matt Lukac
- Murillo Rodrigues
- Victoria Caudill
- Anastasia Teterina
- Jeff Adrion
- CJ Battey
- Jared Galloway
- the rest of the Co-Lab
Funding:
- NIH NIGMS
- NSF DBI
- Sloan foundation
- UO Data Science
- Jerome Kelleher
- Ben Haller
- Ben Jeffery
- Georgia Tsambos
- Jaime Ashander
- Gideon Bradburd
- Madeline Chase
- Bill Cresko
- Alison Etheridge
- Evan McCartney-Melstad
- Brad Shaffer
- Sean Stankowski
- Matt Streisfeld